Лінійна залежність та незалежність. Вимірність простору. Базис

Означення: Елементи 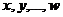 лінійного простору  називаються лінійно залежними, якщо існують такі числа , не всі рівні нулю, що

                                                                         (6)                           

  Означення: Елементи 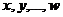  лінійного простору  називаються лінійно незалежними, якщо з рівності

, слідує, що  .

Означення: Нескінченна система елементів  простору  називається лінійно незалежною,  якщо будь-яка її скінчена підсистема лінійно незалежна.

Означення: Якщо в просторі  можна знайти  лінійно незалежних елементів, а будь-які  елементів цього простору лінійно залежні, то говорять, що   має вимірність .

Означення: Якщо ж в  можна вказати систему з довільного скінченного числа лінійно незалежних елементів, то говорять, що простір   нескінченно вимірний.

Означення: Базисом  в - вимірному просторі  називається будь-яка підсистема з   лінійно незалежних елементів.

Простори  і 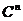 мають вимірність , простори - нескінченновимірні.

 

Лінійний многовид (лінійна многостатність).

 

  Означення: Підмножина  лінійного простору   називається лінійним підпростором, якщо вона сама утворює лінійний простір по відношенню до визначених в  операцій додавання і множення на число.

Означення: Не порожня підмножина  лінійного простору   називається лінійним многовидом (лінійною многостайністю), якщо з того, що  слідує , для будь-яких чисел .

У будь-якому лінійному просторі  існує два «тривіальних» підпростори: перший складається з одного нульового вектора (і тому називається нульовим підпростором), другий збігається зі всім .

 Також, у будь-якому лінійному просторі є лінійний многовид який збігається зі всім .

Означення: Підпростір, який складається з хоч би одного не нульового елемента називається власним підпростором.

 

Приклади многовидів.

1). Нехай - лінійний простір, деякий його елемент. Сукупність , де  пробігає всі числа (дійсні або комплексні), створює лінійний многовид.

2). Розглянемо простір , у ньому сукупність многочленів  створює лінійний многовид. В той же час, сам простір  можна розглядати, як лінійний многовид більш широкого простору всіх неперервних та розривних функцій на .

3). Розглянемо простори , кожний з них є лінійним многовидом у наступному просторі.

Твердження: Нехай  - довільна не порожня множина елементів лінійного простору . Тоді в  існує найменший лінійний многовид (який можливо співпадає с ), який містить  .

Доведення. Дійсно, є майже один лінійний многовид,), який містить , це сам простір . Зрозуміло, що перетин будь-якої множини лінійних многовидів  є лінійний многовид. Дійсно, якщо  і , то ,отже , , то 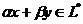, . Візьмемо зараз всі лінійні многовиди, які містить систему векторів та розглянемо їх перетин. Це й буде найменший лінійний многовид, який містить .

Означення: Найменший лінійний многовид, який містить систему елементів , називається лінійним многовидом, породженим множиною , або лінійною оболонкою множини .

Позначають лінійну оболонку - .

Зміст

1. Лінійні простори………………………………………………….

2. Приклади лінійних просторів…………………………………..

3. Ізоморфізм…………………………………………………………

4. Лінійна залежність та незалежність. Базис…………………...