Агрегат как универсальная математическая схема

Для описания систем

Рассмотренные математические схемы позволяют дать форма­лизованное описание системы и в ряде случаев получить аналити­ческие решения. Однако эти схемы не дают представления о струк­туре имитационного алгоритма, что необходимо, если такой способ выбран в качестве метода исследования. Эта структура становится очевидной при использовании такой общей универсальной математической схемы, как агрегат. Одно из первых описаний агрегата можно найти в монографии Н.П. Бусленко [1].

Для задания агрегата вводят следующие множества: Т — фик­сированное подмножество множества действительных чисел; X, Г, Y, Z — множества любой природы. Элементы указанных множеств определяются так: — момент времени;  — входной,  — управляющий,  — выходной сигналы; — состоя­ние. Впоследствии состояния, входные, выходные и управляющие сигналы будут рассматриваться как функции времени; их значения в момент t будут обозначаться z(t), x(t), y(t), g(t) соответственно.

Под агрегатом понимается абстрактный объект, определяе­мый множествами Т, X, Г, Y, Z и операторами (вообще говоря, слу­чайными) переходов V и выходов W, реализующими функции z(t) и y(t) соответственно. Агрегат характеризуется также пространством параметров агрегата П, элементы которого имеют вид .

Рассмотрим реализацию оператора выходов W. Этот оператор строится следующим образом.

В пространстве состояний агрегата Z для каждого значения  и  можно выделить некоторую область , вид которой зависит от g и . Если траектория системы z (f) попадает в эту область, то надлежит выдать выходной сигнал. Множество 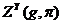 в общем случае изменяется при изменении параметров аг­регата и в моменты поступления новых управляющих сигналов g(t). В интервалах времени между моментами поступления управ­ляющих сигналов множество  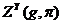не изменяется и остается та­ким, каким оно оказалось в момент поступления последнего управ­ляющего сигнала.

Множество 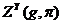 определяет вид и моменты выдачи выход­ных сигналов.

Формально это можно записать следующим образом. Если при , где — интервал времени дос­таточно малой длительности, но , то момент t является моментом выдачи выходного сигнала

            (2.4)

В общем случае оператор W " является случайным оператором. Это значит, что данным t, z(t), g(t) и ставится в соответствие не одно определенное значение у, а некоторое множество Y с распре­делением вероятностей, задаваемых оператором W ". Оператор  «следит» за попаданием траектории агрегата в область 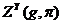и определяет очередной момент достижения процессом z(t) подмно­жества 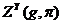. Этот момент является моментом выдачи выходного сигнала.

Итак, оператор W ' вырабатывает очередные моменты выдачи выходных сигналов, а оператор W " формирует содержание этих сигналов.

Обратимся теперь к оператору переходов V. Наряду с непрерыв­ным изменением состояния агрегата z(t) будем рассматривать так­же «скачкообразные» изменения его состояния. Такие переходы имеют место, когда агрегат выдает выходной сигнал или принима­ет входной сигнал, или получает управляющий сигнал. Состояния, в которые переходит агрегат в этих случаях, называют «особыми» состояниями и обозначают как z(t + 0), указывая таким образом, что это то состояние, в которое агрегат переходит за бесконечно малый интервал времени, т.е. скачком. Так работают, например, дискретные электронные элементы.

Вид оператора V зависит от следующих факторов: а) поступили или нет в течение рассматриваемого интервала времени управ­ляющие и входные сигналы; б) был ли выдан выходной сигнал. Поэтому представим его в виде совокупности случайных операто­ров V*, V', V" и U.

Пусть t' — момент поступления в агрегат входного сигнала х'. Тогда агрегат, находившийся в этот момент в состоянии z(t'), пере­ходит в состояние

  (2.5)

Здесь под g понимается последний управляющий сигнал, посту­пивший в момент     t < .                                                           

Если t "— момент поступления в агрегат управляющего сигнала , то

(2.6)

Если t — момент одновременного поступления в агрегат и входного х, и управляющего g сигналов, то

(2.7)

В этом выражении под понимается не оператор, а результат его действия на аргументы t, z(t), g, . Другими слова­ми, вместо (2.7) можно записать

где  определяется соотношением (2.6) для t, z(t), g, .

Если оператор W ' обнаружил, что в момент t * есть условия для выдачи выходного сигнала у, то, выдав этот сигнал, агрегат перей­дет в особое состояние

  (2.8)

Здесь под g понимается последний управляющий сигнал, посту­пивший в момент t<t*.

Если полуинтервал не содержит моментов поступления входных и управляющих сигналов или выдачи выходных сигна­лов, а  — момент следующего «особого» состояния, тс для  имеет место непрерывное изменение: состояния агрегата

(2.9)

причем — последний управляющий сигнал, поступивший в момент t < . Заметим, что обозначение  указывает на то, что вид оператора U зависит от того, каким было последнее особое состояние.                

Рассмотренная математическая схема позволяет описывать широкий класс систем, поскольку в ней предусмотрено:

наличие разных типов внешних сигналов (не только информа­ционных х, но и управляющих g), что позволяет имитировать из­менение алгоритма работы исследуемой системы;

непрерывное изменение состояний системы z(t),

«скачкообразное» изменение состояний системы z(t + 0);

вероятностный характер реакции системы на внешние сигналы.

С помощью соотношений (2.5)-(2.9) можно описать процесс функционирования агрегата (см. подробнее, например, [1, 11]), a затем построить алгоритм, имитирующий этот процесс.