Вообще, говорят, что проблема распознавания какого-либо свойства разрешима, если существует допускающий механическое вычисление тест (вычислимая, или эффективная, процедура), который, будучи применен к произвольному объекту соответствующего типа, по прошествии некоторого времени правильно классифицирует этот объект с точки зрения наличия или отсутствия у него некоторого свойства. (Слова «по прошествии некоторого времени» означают здесь «после некоторого конечного числа шагов».) Позитивным тестом называется эффективная процедура, устанавливающая по прошествии некоторого времени все случаи наличия соответствующего свойства и только их. Негативный тест – это эффективная процедура, обнаруживающая все случаи отсутствия свойства и только их. Проблема распознавания произвольного свойства разрешима тогда и только тогда, когда для него существует и позитивный, и негативный тесты; дело в том, что всякий объект может или обладать рассматриваемым свойством, или нет, и потому, обладая обоими тестами, можно применить их оба к интересующему объекту, выполняя поочередно шаги одного и другого, и после некоторого их количества обнаружить, обладает он этим свойством или нет. (Верно и обратное: всякий тест, устанавливающий через некоторое конечное число шагов, обладает данный объект рассматриваемым свойством или нет, реализует и позитивный, и негативный тесты для этого свойства) Нас будут интересовать сейчас свойства общезначимости и выполнимости, а в роли объектов «соответствующего типа» выступают формулы языка логики первого порядка.
Докажем, что для этих тестов не существует дополнительных – позитивного для выполнимости и негативного для общезначимости – и потому в логике первого порядка проблемы распознавания как общезначимости, так и выполнимости неразрешимы.
Докажем неразрешимость логики первого порядка от противного: покажем, что если бы соответствующий тест существовал, то проблема остановки оказалась бы разрешимой. Мы убедились, что проблема остановки неразрешима.
Наше доказательство от противного будет строиться так: мы покажем, как, располагая программой машины Тьюринга, а также натуральным числом n, можно эффективно построить такие конечное множество предложений Д и еще одно предложение Н, что Д ├ Н тогда и только тогда, когда рассматриваемая машина, будучи запущенной в состоянии n (т.е. когда она начинает работу в состоянии q 1, считывая при этом самую левую единицу в сплошном массиве из n единиц на ленте с пустыми символами в остальных клетках), в конце концов останавливается. Таким образом, мы определяем некоторую интерпретацию машины Тьюринга I. Формула Н в интерпретации I говорит, что машина в конце концов остановится, а формула из множества Д описывают работу машины. Введем функцию следования ' (где i' = i + 1 для всякого i). Таким образом, если бы мы могли решить проблему распознавания общезначимости предложений, мы смогли бы эффективно решать, остановится в конце концов или нет данная машина Тьюринга, поскольку логическое следование Д ├ Н имеет место тогда и только тогда, когда общезначима импликация F1  F2
F2  …
…  Fk→H, где Fi
Fk→H, где Fi  Д (i = 1,2,… k).
Д (i = 1,2,… k).
Будем считать, что клетки ленты машины Тьюринга занумерованы так:
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
Будем также предполагать, что время разбито на бесконечную последовательность моментов t, в каждый из которых машина выполняет точно одну свою операцию, и что машина начинает работу в момент времени 0, считывая при этом содержимое клетки 0. Моменты времени предполагаются неограниченно продолжаемыми как в будущее, так и в прошлое, равно как и лента бесконечно простирается и вправо, и влево. Мы считаем, что машина «включается» в момент 0 и «выключается» в первый момент (если таковой наступит), который следует за моментом ее остановки; мы считаем, далее, что во все отрицательные моменты времени и во все моменты, следующие за моментом остановки машины, она не находится ни в каком состоянии, не считывает никакую из имеющихся клеток и никакой символ (даже пустой) не встречается нигде на ее ленте.
Каждому состоянию q i, в котором может пребывать машина, ставится в соответствие некоторый двуместный предикатный символ Qi, подобным же образом каждому символу a j, который машина может считывать либо записывать, ставится в соответствие двуместный предикатный символ Aj. Помимо символов Qi и Aj в формулах из множества Д  {Н} могут встречаться только следующие символы: имя 0, одноместный функциональный символ ' и двуместный предикатный символ <.
{Н} могут встречаться только следующие символы: имя 0, одноместный функциональный символ ' и двуместный предикатный символ <.
В предполагаемой интерпретации I предложений из множества Д  {Н} предметной областью являются целые числа. Имени 0 интерпретация I приписывает значение нуль, а функциональному символу ' – функцию следования. Символы Qi, Aj и < интерпретируются следующим образом:
{Н} предметной областью являются целые числа. Имени 0 интерпретация I приписывает значение нуль, а функциональному символу ' – функцию следования. Символы Qi, Aj и < интерпретируются следующим образом:
I объявляет Qi истинным на паре t, x в точности тогда, когда машина в момент времени t находится в состоянии q i, считывая при этом клетку с номером х.
I объявляет a j истинным на паре t, x в точности тогда, когда вмомент t в клетке с номером х находится символ a j;
I объявляет < истинным на паре х, у в точности тогда, когда х меньше чем у.
Выясним теперь, какие функции содержатся в множестве Д. (Будем использовать переменную t в тех случаях, когда имеется в виду время, и переменные х и у, когда речь идет о клетках на ленте.) Пусть a i, …, a n – список символов, считываемых и записываемых машиной. Для каждой строки программы вида q i a j → a pC q k мы включаем в множество Д формулу
(1) " x " y " t ((t Qi x  t Aj x) → (t ' Qk x
t Aj x) → (t ' Qk x  t Ap x
t Ap x  (y ≠ x → (t A0 y → t 'A0 y
(y ≠ x → (t A0 y → t 'A0 y  …
…  t An y → t 'An y))))
t An y → t 'An y))))
(«Если в момент времени t машина находится в состоянии q i, считывая при этом символ a j в клетке х, то в момент t + 1 машина перейдет в состояние q k, считывая при этом клетку х, в которой появится символ Ap, а во всех клетках, отличных от х, в момент t + 1 останутся те же символы, что в момент t для всех t и х.»)
Также в множество Д для каждой строки программы вида q i a j → a j П q k мы включаем формулу
(2) " x " y " t ((t Qi x  t Aj x) → (t ' Qk x '
t Aj x) → (t ' Qk x '  (t A0 y → t 'A0 y)
(t A0 y → t 'A0 y)  …
…  (t An y → t 'An y)))
(t An y → t 'An y)))
(«Если в момент времени t машина находится в состоянии q i, считывая при этом символ a j в клетке х, то в момент t + 1 машина перейдет в состояние q k, считывая при этом клетку х + 1, и во всех клетках в момент t + 1 останутся те же символы, что в момент t для всех t и х.»)
Аналогично для строк вида q i a j → a jЛ q kвключаем в Д
(3) " x " y " t ((t Qi x '  t Aj x ') → (t ' Qk x
t Aj x ') → (t ' Qk x  (t A0 y → t 'A0 y)
(t A0 y → t 'A0 y)  …
…  (t An y → t 'An y)))
(t An y → t 'An y)))
(«Если в момент времени t машина находится в состоянии q i, считывая при этом символ a j в клетке х + 1, то в момент t + 1 машина перейдет в состояние q k, считывая при этом клетку х, и во всех клетках в момент t + 1 останутся те же символы, что в момент t для всех t и х.»)
Одно из предложений множества Д утверждает, что в начальный момент машина находится в состоянии q 1, считывая при этом самую левую единицу в сплошном массиве единиц на ленте с пустыми символами в остальных клетках:
(4) 0 Qi 0  0 A1 0
0 A1 0  0 A1 0'
0 A1 0'  …
…  0 A1 0(n-1)
0 A1 0(n-1)  " y ((y ≠ 0
" y ((y ≠ 0  y ≠ 0'
y ≠ 0'  …
…  y ≠ 0(n-1)) → 0 A0 y)
y ≠ 0(n-1)) → 0 A0 y)
Здесь 0(n-1) обозначает результат применения n символов следования к символу 0.
Еще одна из формула множества Д утверждает, что всякое целое число является следующим точно за одним целым:
(5) " z $ x z = x '  " z " x " y (z = x '
" z " x " y (z = x '  z = y ' → x = y)
z = y ' → x = y)
Введем в Д еще одну формулу
(6) " x " y " z (x < y  y < z → x < z)
y < z → x < z)  " x " y (x ' = y → x < y)
" x " y (x ' = y → x < y)  " x " y (x < y → x ≠ y),
" x " y (x < y → x ≠ y),
из которого следует, что если p и q – различные натуральные числа, то " x x (p) ≠ x (q).
Таким образом, Д состоит из формул (1), (2), (3), соответствующих всем командам машины, и трема дополнительными (4), (5), (6). Что касается предложения Н, то заметим, что всякая машина останавливается в момент времени t, если она в это время находится в состоянии q i, считывая при этом символ a j, причем в машинной таблице нет команды, соответствующей комбинации q i a j. Таким образом, за предложение Н мы принимаем дизъюнкцию всех предложений вида
$ t $ x (t Qi x  t Ai x),
t Ai x),
для которых в машинной таблице нет команд, соответствующих комбинациям q i a j. Если же для всякой такой комбинации в таблице имеются команды, то машина никогда не остановится, и за Н в этом случае мы принимаем какую-либо формулу, ложную в интерпретации I, например 0 ≠ 0.
Мы показали, как по данной машине и входному значению n построить такие конечное множество предложений Д и отдельное предложение Н, что соотношение Д ├ Н имеет место тогда и только тогда, когда машина, получив n на входе, в конце концов, останавливается.
Рассмотрим факты, касающиеся отношения ├ в логике первого порядка. Все предложения из множества Д истинны в интерпретации I. Поэтому если Д ├ Н, то и Н истинно в I. Но Н истинно в I тогда и только тогда, когда машина, получив на входе n, в конце концов останавливается.
Введем теперь один специальный тип формул, называемых нами описаниями времени s. Так называется всякая формула, определяющая очевидным способом, в каком состоянии находится машина в момент s, какая клетка ею в это время считывается, а также в каких клетках ленты какие символы записаны, причем все это делается на языке множества формул Д  {Н}. Точнее говоря, всякое описание времени s есть формула вида
{Н}. Точнее говоря, всякое описание времени s есть формула вида
(7) 0(s)Qi0(p)  0(s)
0(s) 
 …
…  0(s)Aj0(p)
0(s)Aj0(p)  …
…  0(s)
0(s) 
 " y ((y
" y ((y 

 …
…  y
y  0(p)
0(p)  …
…  y
y 
 ) → 0(s)A0 y)
) → 0(s)A0 y)
Мы требуем при этом, чтобы последовательность целых чисел p1,…, р,…, pv была возрастающей; р может совпадать с р1 или с рv Заметим, что формула (4) является описанием времени 0.
Предположим теперь, что машина, получив на входе число n, в конце концов останавливается. Тогда для некоторых s, i, p и j машина в момент s окажется в состоянии qi, считывая при этом клетку с номером р, содержащую символ aj, причем в программе машинной нет команды для комбинации q i a j.
Предположим, далее, что из множества формул Д следует некоторое описание G времени s. Поскольку I – модель для Д, формула G должно быть истинным в I. Поэтому G должно содержать в качестве конъюнктивных членов формулы 0(s)Qi0(p) и 0(s)Aj0(p) а потому из G должна следовать формула
$ t $ x (t Qi x  t Ai x),
t Ai x),
входящее одним из дизъюнктивных членов в H. Поэтому Н будет следовать из Д.
Остается лишь показать, что для всякого неотрицательного s, если только машина не останавливается до момента s, из Д следует некоторое описание времени s. Докажем это индукцией по s.
Основание индукции. Пусть s = 0. Множество Д содержит, а потому и влечет за собой предложение (4), являющееся описанием времени 0.
Шаг индукции. Предположим, что выделенное курсивом предложение верно (для s). Предположим, далее, что наша машина не остановилась до момента s + 1. Это значит, что она не остановилась ни до момента s, ни в самый момент s. Тогда из Д следует некоторое описание (8) времени s. Нужно доказать, что из Д следует и некоторое описание времени s+1.
Поскольку I – модель для Д, формула (8) истинна в I. Поэтому в момент s машина находится в состоянии qi, считывая при этом некоторую клетку (с номером р), в которой записан символ aj. Поскольку машина в момент s не остановилась, в ее программе должна присутствовать команда одного из видов
(a) q i a j → a k С q m
(б) q i a j → aj П q m
(в) q i a j → aj Л q m
Если имеется команда типа (а), то одна из формул множества Д есть
" x " y " t ((t Qi x  t Aj x) → (t ' Qk x
t Aj x) → (t ' Qk x  t Ap x
t Ap x  (y ≠ x → (t A0 y → t 'A0 y
(y ≠ x → (t A0 y → t 'A0 y  …
…  t An y → t 'An y))))
t An y → t 'An y))))
Она вместе с (5), (6) и (8) влечет за собой формулу
0 (s+1) Qi0 (p)  0 (s+1) Aj10 (p1)
0 (s+1) Aj10 (p1)  …
…  0 (s+1) Aj0 (p)
0 (s+1) Aj0 (p)  …
…  0 (s+1) Ajv0 (pv)
0 (s+1) Ajv0 (pv)  " y ((y ≠ 0 (p1)
" y ((y ≠ 0 (p1)  …
…  y ≠ 0 (p)
y ≠ 0 (p)  …
…  y ≠ 0 (pv)) → 0 (s+1) A0 y),
y ≠ 0 (pv)) → 0 (s+1) A0 y),
являющуюся описанием времени s + 1.
Еcли имеется команда типа (б), то одна из формул множества Д есть
" x " y " t ((t Qi x  t Aj x) → (t ' Qk x '
t Aj x) → (t ' Qk x '  (t A0 y → t 'A0 y)
(t A0 y → t 'A0 y)  …
…  (t An y → t 'An y)))
(t An y → t 'An y)))
Из этого предложения, объединенного с (5), (6) и (8), следует, что для некоторого символа  ,
,
0(s+1)Qi0(p+1)  0(s+1)
0(s+1) 
 …
…  0(s+1)Aj0(p+1)
0(s+1)Aj0(p+1)  …
…  0(s+1)
0(s+1) 
 " y ((y ≠
" y ((y ≠ 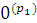
 …
…  y ≠ 0(p+1)
y ≠ 0(p+1)  …
…  y ≠
y ≠  ) → 0(s+1)A0 y),
) → 0(s+1)A0 y),
а это предложение является описанием времени s + 1.
Если имеется стрелка типа (в), то одна из формул множества Д есть
" x " y " t ((t Qi x '  t Aj x ') → (t ' Qk x
t Aj x ') → (t ' Qk x  (t A0 y → t 'A0 y)
(t A0 y → t 'A0 y)  …
…  (t An y → t 'An y)))
(t An y → t 'An y)))
Тогда существует такой символ a q, что из последней формулы, объединенной с (5), (6), (8), следует
0(s+1)Qi0(p-1)  0(s+1)
0(s+1) 
 …
…  0(s+1)Aj 0(p-1)
0(s+1)Aj 0(p-1)  …
…  0(s+1)
0(s+1) 
 " y
" y
((y 
 y
y  0(p-1)
0(p-1)  …
…  y
y 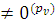 ) → 0(s+1)A0 y)
) → 0(s+1)A0 y)
а это предложение является описанием времени s + 1.
Во всех трех случаях множество Д имеет следствием некоторое описание времени s + 1, и тем самым неразрешимость логики первого порядка доказана.
 2020-01-14
2020-01-14 168
168








