2020-01-15
144
Оглавление
Оглавление. 2
Список обозначений ко всей выпускной работе. 4
Реферат на тему «Применение ИТ при решении задач теории графов». 5
Введение. 5
Глава 1 Базовые понятия теории графов. 6
1.1 Основные определения. 6
Глава 2 Анализ GraphMagic: системы работы с графовыми моделями и алгоритмами. 9
2.1 Основные преимущества системы GraphMagic. 9
Глава 3 Плагин для системы GraphMagic. 18
3.1 Описание плагина. 18
3.2 Используемые технологии. 18
3.2.1 Java. 18
3.2.2 Swing. 21
3.3 Результаты работы плагина. 23
Заключение. 25
Список литературы к реферату. 25
Предметный указатель к реферату. 27
Интернет ресурсы в предметной области исследования 28
Действующий личный сайт в WWW... 29
Граф научных интересов.. 30
Тестовые вопросы по Основам информационных технологий.. 32
Презентация магистерской диссертации.. 33
Список литературы к выпускной работе. 34
Приложение. 35
Список обозначений ко всей выпускной работе
AI – искусственный интеллект
ИТ – информационные технологии.
СВГ – системы визуализации графов
ТГ – теория графов
ЭВМ – электронная вычислительная машина
Реферат на тему «Применение ИТ при решении задач теории графов»
Введение
Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждение о Кенигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины 19 века и был сосредоточен главным образом в Англии. Имелось много причин для такого оживленного изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул.
20-е столетие было свидетелем неуклонного развития теории графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.
Таким образом, теория графов стала существенной частью математического аппарата кибернетики, языком дискретной математики. В значительной степени через теорию графов происходит ныне проникновение математических методов в науку и технику.
Одним из примеров использования теории графов является проектирование сетей и передача информации. Для этой задачи надежность является основным принципом функционирования. Сеть должна быть спроектирована таким образом, чтобы при выходе из строя её отдельных элементов функциональность сети не нарушалась. Естественным образом возникает задача нахождения реберно-непересекающихся цепей между выделенными узлами. Стоимость всей сети должна быть минимальна при условии её надежности. Таким образом, при решении задачи проектирования возникают следующие подзадачи:
o Построение кратчайшей пары реберно-непересекающихся путей между двумя вершинами;
o Построение K(K>2) кратчайшего множества реберно-непересекающихся путей между двумя вершинами.
Целью данного проекта является разработка плагина для системы GraphMagic, который поможет решать вышеперечисленные задачи, а также поможет специалистам, студентам и другим заинтересованным в теории графов людям работать с графовыми моделями и алгоритмами.
Глава 1 Базовые понятия теории графов
Основные определения
Термин «граф» впервые появился в книге выдающегося венгерского математика Д. Кёнига в 1936г.
Пусть V — непустое множество, V (2) — множество всех его двухэлементных подмножеств. Пара (V, Е), где Е — произвольное подмножество множества V (2), называется графом (неориентированным графом).
В этой работе рассматриваются только конечные графы, т. е. множество V предполагается конечным, хотя в определении графа конечность этого множества не требуется. Элементы множества V называются вершинами графа, а элементы множества E — ребрами. Итак, граф — это конечное множество V вершин и множество E ребер, E Í V (2). Множества вершин и ребер графа G обозначаются символами VG и EG соответственно. Вершины и ребра графа называются его элементами. Число | VG| вершин графа G называется его порядком и обозначается через | G|. Если | G| = n, |EG| = m, то G называют (n, m)-графом.
Говорят, что две вершины u и v графа смежны, если множество { и, v }является ребром, и не смежны в противном случае. Если e = { и, v }— ребро, то вершины u и v называют его концами. В этой ситуации говорят также, что ребро e соединяет вершины u и v. Такое ребро обозначается символом uv.
Два ребра называются смежными, если они имеют общий конец.
Вершина u и ребро e называются инцидентными, если v является концом ребра e (т. е. e = иv), и не инцидентными в противном случае.
Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Множество всех вершин графа G, смежных с некоторой вершиной v, называется окружением вершины v и обозначается через NG (v)или просто N (v).
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии — ребрам
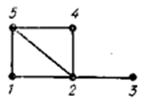
Иногда приведенное выше определение графа оказывается недостаточным и приходится рассматривать более общие объекты, в которых две вершины могут соединяться более чем одним ребром. Так возникает понятие «мультиграф». Мультиграф — это пара (V, E), где V — непустое множество (вершин), а E — семейство подмножеств множества V (2) (ребер). Употребление термина «семейство» вместо «множество» означает, что элементы множества V (2) могут в E повторяться, т. е. допускаются кратные ребра.
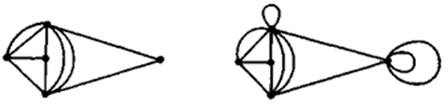
Дальнейшее обобщение состоит в том, что кроме кратных ребер допускаются еще петли, т. е. ребра, соединяющие вершину саму с собой. Псевдограф — это пара (V, E), где V — непустое множество (вершин), а E —некоторое семейство неупорядоченных пар вершин (ребер), не обязательно различных. На следующих рисунках изображены мультиграф и псевдограф.
Изучаются также ориентированные графы. Тогда множество V (2) двухэлементных подмножеств заменяется декартовым квадратом V 2, состоящим из упорядоченных пар элементов множества V. Итак, ориентированный граф (или орграф) — это пара (V, A), где V — множество вершин, A — множество ориентированных ребер, которые называются дугами, A 
V2. Если a = (v 1, v 2)— дуга, то вершины v 1и v 2называются ее началом и концом соответственно. На рисунке дуги отмечаются стрелками, указывающими направление от начала к концу. Аналогично определяется ориентированный мультиграф. Рассматриваются также смешанные графы, у которых есть и дуги, и неориентированные ребра.
Простой граф, в котором каждая пара вершин смежна называется полным. Полные графы обозначаются Kn. На рисунке ниже изображены полные графы K1, K2, K3, K4.
Граф называется двудольным, если существует такое разбиение его вершин на две части (доли) такие, что концы каждого ребра принадлежат разным частям. Полный двудольный граф, доли которого состоят из p и q вершин, обозначается символом Kp,q. На рисунке ниже изображены полные двудольные графы K1,4, K3,3.
Два графа называются изоморфными, если между множеством их вершин существует такое взаимнооднозначное соответствие, при котором в одном из графов вершины соединены ребрами только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг также должна быть одинаковой. Отношение изоморфизма является эквивалентностью, т. к. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы одного класса изоморфны, а графы разных классов не изоморфны.
Глава 2 Анализ GraphMagic: системы работы с графовыми моделями и алгоритмами
