Периодические функции

Функция f (x) называется периодической с периодом T ≠ 0, если выполняются два условия:

· если 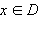, то x + T и x – T также принадлежат области определения D (f (x));

· для любого 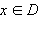выполнено равенство

f (x + T) = f (x).

Поскольку то из приведенного определения следует, что f (x – T) = f (x).

Если T – период функции f (x), то очевидно, что каждое число nT, где , n ≠ 0, также является периодом этой функции.

Наименьшим положительным периодом функции называется наименьшее из положительных чисел T, являющихся периодом данной функции.

График 1.3.4.1. График периодической функции

График периодической функции обычно строят на промежутке [x₀; x₀ + T), а затем повторяют на всю область определения.

Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π), y = tg x (период равен π) и другие. Функция y = const также является периодической. Для нее периодом является любое число T ≠ 0.

1

Рисунок 1.3.4.1. Не следует думать, что периодическими бывают только тригонометрические функции. Функция y = [x], где [x] – целая часть числа x (наибольшее целое число, не превосходящее x) позволяет определить функцию y = {x}, где {x} – дробная часть числа x. По определению {x} = x – [x] (например, {3,7} = 0,7, {–6} = 0, {–4,2} = –4,2 – (–5) = 0,8). Дробная часть числа – функция с периодом T = 1.

В заключение отметим свойства периодических функций.

· Если f (x) – периодическая функция с периодом T, то функция g (x) = A · f (kx + b), где k ≠ 0 также является периодической с периодом .

· Пусть функции f₁ (x) и f₂ (x) определены на всей числовой оси и являются периодическими с периодами T₁ > 0 и T₂ > 0. Тогда если то функция периодическая с периодом T, равным наименьшему общему кратному чисел

Монотонность функций

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

1

Рисунок 1.3.5.1. Промежутки возрастания и убывания функции.

На показанном на рисунке графике функция y = f (x), возрастает на каждом из промежутков [a; x₁) и (x₂; b] и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁) и (x₂; b], но не на объединении промежутков

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

· Сумма нескольких возрастающих функций является возрастающей функцией.

· Произведение неотрицательных возрастающих функций есть возрастающая функция.

· Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.

· Если функция f возрастает и сохраняет знак, то функция 1/f убывает.

· Если функция f возрастает и неотрицательна, то где , также возрастает.

· Если функция f возрастает и n – нечетное число, то f ⁿ также возрастает.

· Композиция g (f (x)) возрастающих функций f и g также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

Модель 1.9. Свойства функции.

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого 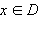(x ≠ a) выполняется неравенство f (x) ≤ f (a) то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого 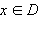(x ≠ b) выполняется неравенство f (x) > f (b) то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

График 1.3.5.1. Функция, ограниченная сверху.

График 1.3.5.2. Функция, ограниченная снизу.

График 1.3.5.3. Функция, ограниченная на множестве D.

Если существует число C такое, что для любого 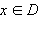выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D.

Если существует число c такое, что для любого 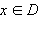выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), лежит в полосе c ≤ y ≤ C.

Если функция не является ограниченной на множестве, то говорят, что она не ограничена.

Примером функции, ограниченной снизу на всей числовой оси, является функция y = x². Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.