Данный метод для минимизации функции в коде Грея. В каждую ячейку записывается значение функции на данном наборе. Затем выделяются группы ячеек размером 2a*2b, где a, bε[0,1,2…], в которых функция принимает значение «1». В каждую группу должно входить максимальное число ячеек. Таких групп должно быть минимальное количество. Каждой группе будет соответствовать конъюнктивный член размером n-a-b. Для получения МДНФ каждую группу надо просматривать в горизонтальном и вертикальном измерениях, с нахождения таких переменных, которые не меняют своего значения в пределах группы. Если переменная не меняет своего нулевого значения, то она вписывается в конъюнкцию с отрицанием, если не меняет своего единичного значения, то вписывается без отрицания. Если имеются разорванные группы, то карту Карно надо свернуть в цилиндр. На неопределенных наборах следует доопределить нулем или единицей, в соответствии с выбираемой группой ячеек. Каждая единичная ячейка должна быть включена хотя бы в одну группу.
Составим карту Карно для функции У3 (рисунок 2.3.1).
| x3x4 | |||||
| x1x2 | 00 | 01 | 11 | 10 | |
| 00 | 1 | 1 | |||
| 01 | 1 | ||||
| 11 | 1 | 1 | |||
| 10 | 1 | 1 | |||
Рис. 2.3.1 Карта Карно для функции У3
Таким образом, для функции У3 в МДНФ будет иметь следующий вид:
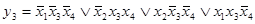
 2020-01-15
2020-01-15 110
110








