2020-01-15
129
Найдём изображения каждого из слагаемых дифференциального уравнения:
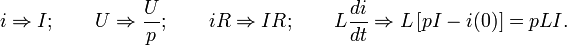
Получаем следующее изображение дифференциального уравнения
Из последнего выражения найдём изображение тока:
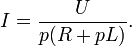
Таким образом, решение сводится к нахождению оригинала тока по известному изображению. Разложим правую часть уравнения на элементарные дроби:
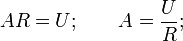
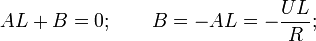
Найдём оригиналы элементов последнего выражения:
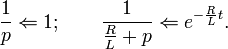
Окончательно получаем
[править] Вывод
Операционное исчисление чрезвычайно удобно в электротехнике для расчёта динамических режимов различных цепей. Алгоритм расчёта следующий.
1) Все элементы цепи рассматриваем как сопротивления Zi, величины которых находим исходя из изображений переходных функций соответствующих элементов.
Например, для резистора:
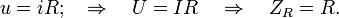
Для индуктивности:
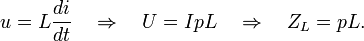
Для ёмкости:
2) Используя указанные значения сопротивлений, находим изображения токов в цепи, используя стандартные методы расчёта цепей, применяемые в электротехнике.
3) Имея изображения токов в цепи, находим оригиналы, которые и являются решением дифференциальных уравнений, описывающих цепь.
|
|
|
[править] Замечания
Интересно отметить, что полученные выше выражения для операторного сопротивления различных элементов с точностью до преобразования
совпадают с соответствующими выражениями для сопротивлений в цепях переменного тока:
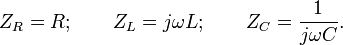
Переходные процессы при включении цепи R, С на постоянное напряжение и
разряде ёмкости на сопротивление.
Обозначим напряжение на зажимах цепи через u, напряжение на обкладках конденсатора через uC, значение его заряда через q
Ri + uC = u.(9.14)
Так как
,
то уравнение (9.14) примет вид
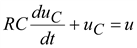. (9.15)
Однородное уравнение цепи
. (9.16)
Характеристическое уравнение: RCp + 1 = 0.
Его корень 
.
Решение однородного уравнения
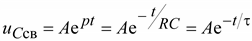. (9.17)
Переходное напряжение:
. (9.18)
Рассмотрим ряд частных случаев.
1. Пусть цепь RC замыкается накоротко, т.е. u = 0 (рис. 9.7).
Для установившегося режима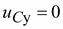 
, и
. (9.19)
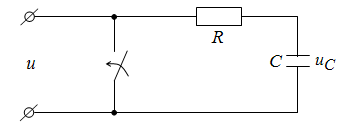
Рис. 9.7. Замыкание RC – цепи накоротко
Пусть к моменту коммутации напряжение на зажимах конденсатора равно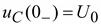 
. Подставив в (9.19) 
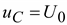и t = 0, получим 
.
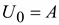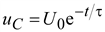(9.20)
Ток в цепи
. (9.21)
Ток в начальный момент скачком повышается от нуля до величины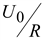 
.
Кривые тока и напряжения на конденсаторе представлены на рис. 9.8.
Энергия, выделяемая в виде теплоты в сопротивлении цепи, равна энергии, запасенной в электрическом поле конденсатора к начальному моменту времени
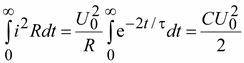. (9.22)
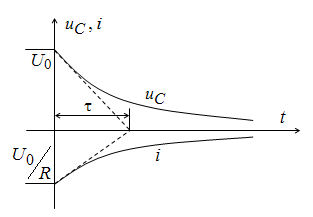
Рис. 9.8. Кривые изменения тока и напряжения на конденсаторе
Постоянная времени τ = RC в реальных устройствах может иметь различные значения (до нескольких суток).
2. Рассмотрим процесс при включении RC цепи под постоянное напряжение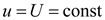 
.
|
|
|
Пусть конденсатор до включения не был заряжен. Установившееся значение напряжения на зажимах конденсатора после завершения переходного процесса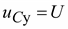 
. Напряжение в переходном процессе
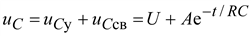. (9.23)
Постоянную интегрирования А определяем из условия 
. Полагая t = 0, получим:
0 = U + A; A = – U.
Общее решение
. (9.24)
Ток в цепи
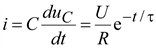. (9.25)
Кривые изменения тока и напряжения на конденсаторе показаны на рис. 9.9.
Количество теплоты, выделившееся в цепи во время заряда, равно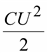 
, что составляет ту же величину, что и при разряде конденсатора. Работа источника внешней ЭДС в этом случае равна CU2, т.е. удвоенному значению энергии, запасаемой в электрическом поле конденсатора.
Рис. 9.9. Кривые изменения тока и напряжения на конденсаторе
Если конденсатор до включения был заряжен, т.е.
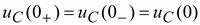, то 
; 
.
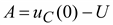Если 
, то конденсатор дозаряжается до напряжения U, а если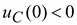 
– перезаряжается от начального отрицательного значения до приложенного напряжения. Соответствующие кривые изображены на рис. 9.10.
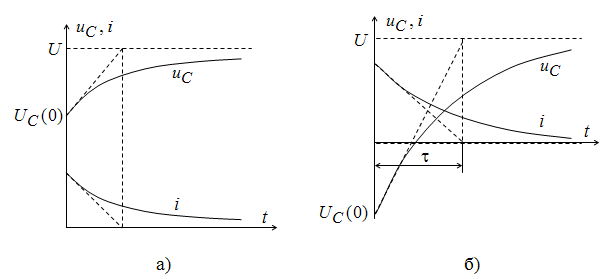
Рис. 9.10. Кривые изменения напряжения на конденсаторе при его дозарядке (а) и перезарядке (б)
3. Рассмотрим процесс включения цепи RC под синусоидальное напряжение 
.
Напряжение uCу в установившемся режиме
,(9.26)
где 
; 
; 
; 
.
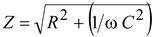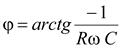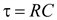Если конденсатор не был заряжен, то 
:
;
.
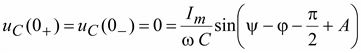Напряжение на конденсаторе будет равно
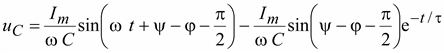. (9.27)
Ток в переходном режиме
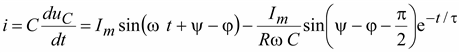. (9.28)
Если конденсатор был предварительно заряжен, то
;
.
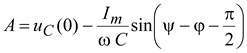Из (9.27) и (9.28) видно, что переходный процесс зависит от величины Ψ.
Если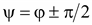 
, то переходный процесс не возникает и сразу же наступает установившийся режим, так как при этом в момент t = 0 установившееся напряжение равно нулю. Таким образом, имеется полное соответствие между запасом энергии в конденсаторе до включения, и запасом энергии, который должен быть в установившемся режиме в этот момент.
Если включение происходит при Ψ = j, то свободное напряжение 
будет наибольшим и в начальный момент имеет значение ImXC. Начальное значение свободного тока при этом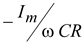 
. Если ωCR > 1, т.е. R < XC, то в начальный момент времени происходит большой всплеск тока, намного превосходящий амплитуду Im. Однако такой большой ток протекает незначительную часть периода, так как 
и τ < T.
Кривые изменения тока при включении конденсатора под переменное напряжение показаны на рис. 9.11.
Рис. 9.11. Кривые изменения тока
Максимальное значение напряжение 
в переходном процессе не превышает удвоенной амплитуды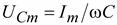 
напряжения на конденсаторе в установившемся режиме.
| Переходные процессы в цепи с последовательно соединенными участками R и L |
Примером такой цепи может служить эквивалентная схема катушки индуктивности, обладающей активным сопротивлением R и индуктивностью L.
Дифференциальное уравнение такой цепи
 ,(9.4)
где u(t) – напряжение на зажимах цепи.
Соответствующее однородное уравнение, определяющее свободный ток:
 .
Характеристическое уравнение
Lp + R = 0
имеет единственный корень p = –R/L. Тогда свободный ток можно вычислить как
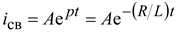 . (9.5)
Выражение установившегося тока iу(t), являющегося частным решением дифференциального уравнения, определяемое видом заданной функции u(t).
Ток в переходном режиме
 .
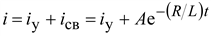Постоянная интегрирования A определяется по начальному значению тока i.
Рассмотрим ряд частных случаев.
1. Пусть цепь в момент t = 0 отключается от источника и замыкается накоротко (рис. 9.1).
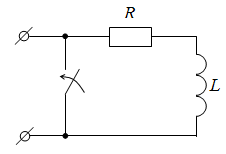Рис. 9.1. Замыкание катушки индуктивности накоротко
После замыкания накоротко u = 0. Установившийся ток в этом случае iу = 0. Тогда полный ток
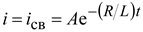 . (9.6)
Начальное условие для определения A: i(0+) = i(0–).
Пусть к моменту коммутации ток в цепи был равен i(0–) = I. Следовательно, i(0+) = I. Полагая в уравнении (9.6) i = I и t = 0, находим I = A.
Решение уравнения имеет вид
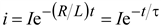 . (9.7)
Величина τ = L/R имеет размерность времени и называется постоянной времени цепи. За промежуток времени t ток уменьшается в e раз. Чем больше τ, тем медленнее затухает ток.
Теоретически ток станет равным нулю через бесконечно большой промежуток времени, практически он становится малым за промежуток времени в несколько значений τ (рис. 9.2).
Постоянная времени τ равна длине подкасательной в любой точке кривой i(t) на рис. 9.2, так как  .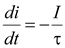
Энергия, выделяемая в виде теплоты в активном сопротивлении R, равна энергии, запасенной в магнитном поле цепи в начальный момент времени
Рис. 9.2. Кривая изменения тока в катушке индуктивности
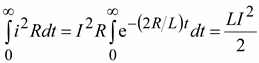 . (9.8)
Постоянная времени τ больших катушек с сердечником может быть весьма значительной. Так, постоянная времени обмотки возбуждения крупных гидрогенераторов может иметь значение 5 с.
2. Рассмотрим процесс отключения от источника постоянного напряжения цепи, состоящей из индуктивной катушки с параметрами R и L и соединенной с ней параллельно ветви с сопротивлением R0(рис. 9.3).
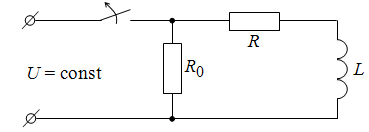Рис. 9.3. Отключение катушки индуктивности
Переходный процесс описывается уравнением
 ,
где  .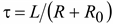
До размыкания рубильника в катушке протекает ток iL(0–) = U/R.
A = iL(0+) = iL(0–) = U/R.
Ток в катушке
 .(9.9)
Напряжение на участке с сопротивлением R0 до размыкания было равно U, а в первый момент времени после размыкания оно окажется равным
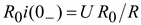 .(9.10)
Если R0 > R, например, на зажимах катушки с сопротивлением R включен вольтметр с большим сопротивлением, то при отключении цепи напряжение на вольтметре в первый момент повысится R0/R раз.
Если энергия магнитного поля, запасенная в катушке достаточно велика, то вольтметр может быть сожжен. Поэтому во избежание возникновения больших перенапряжений при отключении цепей постоянного тока, обладающих большой индуктивностью, например, обмоток возбуждения генераторов, эти цепи предварительно замыкают на малое сопротивление.
3. Рассмотрим процессы при включении RL цепи на постоянное напряжение u = U = const (рис. 9.4).
Ток установившегося режима iу = U/R.
Общий ток в переходном режиме  .
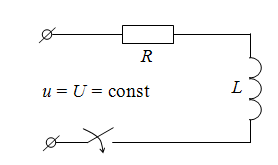Рис. 9.4. Включение катушки индуктивности на постоянное напряжение
Если до включения ток был равен нулю i(0–) = 0, то при t = 0
 .
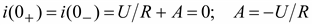Решение уравнения
 .(9.11)
Напряжение на зажимах катушки
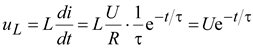 .(9.12)
Кривые изменения тока и напряжения на катушке показаны на рис. 9.5.
4. Рассмотрим процесс при включении цепи под синусоидальное напряжение: .
Ток установившегося режима
 .
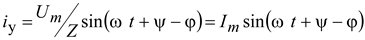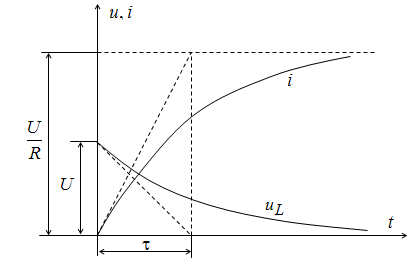Рис. 9.5. Кривые изменения тока и напряжения
Общий ток  ,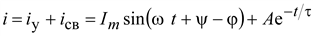
где  .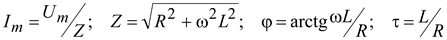
Постоянную интегрирования A определяем из начального условия i(0–) = 0.
i(0+) = i(0–) = Imsin(Ψ – j) + A = 0
Общий ток:
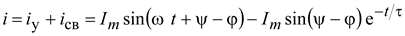 .(9.13)
Кривые изменения тока и напряжения изображены на рис. 9.6.
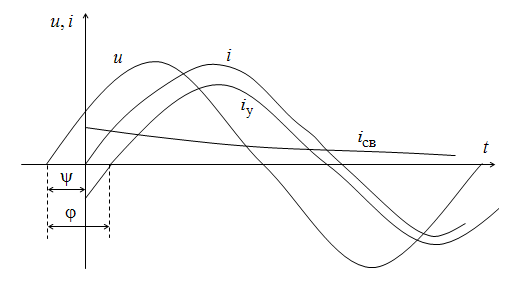Рис. 9.6. Кривые изменения тока и напряжения при включении катушки на синусоидальное напряжение
Начальное значение свободного тока зависит от начальной фазы Ψ напряжения. Наибольшее значение свободного тока, равное амплитуде Im установившегося тока, имеет место, если Ψ – j = +π/2. Наибольшее значение результирующего тока не превышает двойной амплитуды установившегося тока. Свободный ток не возникает, и сразу наступает установившийся режим при условии Ψ = j.
|
|
|
|
|
|
|
Прямое и обратное
преобразования Лапласа.
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию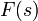 
комплексного переменного (изображение) с функцией 
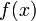вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаютсядифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Определение
[править] Прямое преобразование Лапласа
Преобразованием Лапласа функции вещественной переменной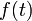 
, называется функция 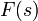комплексной переменной 
[1], такая что:
Правая часть этого выражения называется интегралом Лапласа.
[править] Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного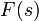 
, называется функция 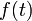вещественной переменной, такая что:
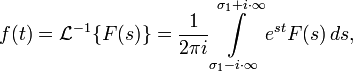
где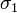 
— некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.
