Как было выяснено в предыдущем пункте, зависимость результативного признака от факторных является прямолинейной. Факторные признаки не являются мультиколлинеарными и практически полностью обуславливают результативный признак, следовательно, все признаки необходимо включить в модель. Поэтому связь будет описываться такой моделью связи (2.5):
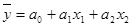 ,(2.5)
,(2.5)
где 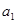 и
и 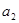 – коэффициенты регрессии.
– коэффициенты регрессии.
Система нормальных уравнений:
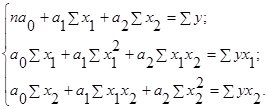 (2.6)
(2.6)
Подставив данные из таблицы 2.1 в эту систему, получается:
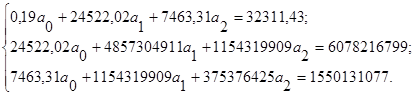
Отсюда: a0 = -2132,16; a1 = 1,005433; a2 = 1,080124;
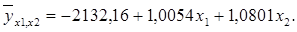
Расчеты показали, что с увеличением себестоимости проданных товаров, продукции, работ, услуг на 1 тыс. руб. и коммерческих, управленческих расходов на 1 тыс. руб. величина выручки от продажи возрастает соответственно в среднем на 1,0054 и 1,0801 тыс. руб.
Далее необходимо проверить адекватность модели, построенной на основе уравнений регрессии.
Во-первых, нужно проверить значимость каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (2.7):
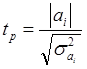 ,
,
(2.7)
где 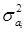 -дисперсия коэффициента регрессии.
-дисперсия коэффициента регрессии.
Параметр модели признается статистически значимым, если
tp > tkp(α; ν=n-k-1),
где α – уровень значимости;
ν – число степеней свободы.
Величина 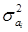 может быть определена по формуле (2.8):
может быть определена по формуле (2.8):
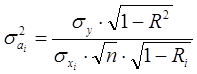 ,(2.8)
,(2.8)
где R – множественный коэффициент корреляции по y;
Ri – множественный коэффициент корреляции по фактору xi с остальными факторами.
В данной работе Ri = 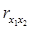 , так как рассматриваются всего два факторных признака.
, так как рассматриваются всего два факторных признака.
По формуле (2.8):
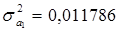 ;
;
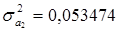 .
.
Теперь по формуле (2.7) определяются значения t-критерия.
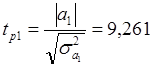 ;
;
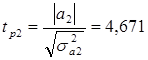 .
.
Оба рассчитанных критерия превышают табличное значение, tkp= 2,12 (0,05; ν=16). Параметры модели являются статистически значимыми.
Во-вторых, проверяется адекватность уравнения регрессии с помощью расчета F-критерия Фишера (2.9):
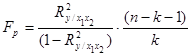 .(2.9)
.(2.9)
Гипотеза о незначимости коэффициента множественной корреляции (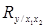 = 0) отвергается, если
= 0) отвергается, если 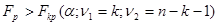 .
.
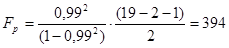 ;
;
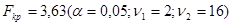 .
.
Гипотеза отклоняется, так как 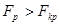 . С вероятностью
. С вероятностью 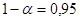 можно сделать заключение о статистической значимости уравнения в целом и показателя тесноты связи
можно сделать заключение о статистической значимости уравнения в целом и показателя тесноты связи 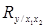 .
.
 2020-01-15
2020-01-15 111
111








