Содержание
Перечень условных обозначений
Введение
1. Необходимые определения и обозначения
2. Используемые результаты
3. Определения, примеры и общие свойства  -перестановочных подгрупп
-перестановочных подгрупп
4. Конечные группы с заданными  -перестановочными подгруппами
-перестановочными подгруппами
Заключение
Список использованных источников
Перечень условных обозначений
 – знак строгого включения множеств;
– знак строгого включения множеств;
 – знак включения множеств;
– знак включения множеств;
 – принадлежность элемента множеству;
– принадлежность элемента множеству;
 – объединение множеств;
– объединение множеств;
 – пересечение множеств;
– пересечение множеств;
 –
–  является подгруппой группы
является подгруппой группы  ;
;
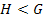 –
–  является собственной подгруппой группы
является собственной подгруппой группы  ;
;
 –
–  является максимальной подгруппой группы
является максимальной подгруппой группы  ;
;
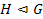 –
–  является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
 –
–  является субнормальной подгруппой группы
является субнормальной подгруппой группы  ;
;
 –
–  является минимальной нормальной подгруппой группы
является минимальной нормальной подгруппой группы  ;
;
Скобки  применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
 – подгруппа, сопряжённая подгрупп
– подгруппа, сопряжённая подгрупп  посредством элемента
посредством элемента  ;
;
 – циклическая группа порядка
– циклическая группа порядка  ;
;
 – симметрическая группа степени
– симметрическая группа степени  ;
;
 – ядро подгруппы
– ядро подгруппы  в группе
в группе  , т.е. пересечение всех подгрупп, сопряжённых с
, т.е. пересечение всех подгрупп, сопряжённых с  в
в  ;
;
 – подгруппа, порожденная всеми подгруппами, сопряженными с подгруппой
– подгруппа, порожденная всеми подгруппами, сопряженными с подгруппой  из
из  элементами
элементами  из
из  , то есть
, то есть 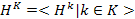 ;
;
 – централизатор множества T в группе G;
– централизатор множества T в группе G;
 – центр группы G;
– центр группы G;
 – нормализатор подгруппы
– нормализатор подгруппы  в группе
в группе  ;
;
 – наибольшая нормальная подгруппа нечетного порядка группы
– наибольшая нормальная подгруппа нечетного порядка группы  ;
;
 – наибольшая нормальная
– наибольшая нормальная  –подгруппа группы
–подгруппа группы  ;
;
 –
–  –холловская подгруппа группы
–холловская подгруппа группы  ;
;
 – силовская
– силовская  –подгруппа группы
–подгруппа группы  ;
;
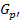 – дополнение к силовской
– дополнение к силовской  –подгруппе в группе
–подгруппе в группе  , т.е.
, т.е.  –холловская подгруппа группы
–холловская подгруппа группы  ;
;
 – группа G изоморфна группе
– группа G изоморфна группе  ;
;
Пусть  – группа,
– группа,  и
и  , тогда:
, тогда:
 – правый смежный класс,
– правый смежный класс,
 – левый смежный класс;
– левый смежный класс;
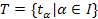 – правая трансверсаль подгруппы
– правая трансверсаль подгруппы 
в группе  ;
;
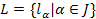 – левая трансверсаль подгруппы
– левая трансверсаль подгруппы 
в группе  ;
;
 – индекс подгруппы
– индекс подгруппы  в группе
в группе  ;
;
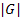 – порядок группы G;
– порядок группы G;
Пусть  и
и  – подгруппы группы
– подгруппы группы  и
и  , тогда:
, тогда:
 – двойной смежный класс группы
– двойной смежный класс группы  по подгруппам
по подгруппам
 и
и  ;
;
 – факторгруппа группы
– факторгруппа группы  по подгруппе
по подгруппе  ;
;
 – прямое произведение подгрупп A и B;
– прямое произведение подгрупп A и B;
 – цоколь группы
– цоколь группы  ;
;
 – коммутатор элементов
– коммутатор элементов  и
и  ;
;
 – коммутант группы G;
– коммутант группы G;
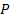 – множество всех простых чисел;
– множество всех простых чисел;
 – дополнение к
– дополнение к  во множестве
во множестве 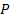 , где
, где  – некоторое множество простых чисел;
– некоторое множество простых чисел;
 –
–  -длина группы
-длина группы  .
.
Введение
Напомним, что подгруппа  группы
группы  перестановочна с подгруппой
перестановочна с подгруппой  , если
, если  . Если
. Если  перестановочна со всеми подгруппами группы
перестановочна со всеми подгруппами группы  , то она называется перестановочной [6] или квазинормальной в
, то она называется перестановочной [6] или квазинормальной в  [7].
[7].
Так как для двух перестановочных подгрупп  и
и  произведение
произведение  также является подгруппой в
также является подгруппой в  , то понятие перестановочных подгрупп является одним из наиболее важных обобщений понятия нормальных подгрупп.
, то понятие перестановочных подгрупп является одним из наиболее важных обобщений понятия нормальных подгрупп.
Перестановочные подгруппы имеют много интересных свойств. Как известно, например, что каждая перестановочная подгруппа является восходящей [8] и, если она является перестановочной подгруппой в некоторой конечной порождённой группе  , то
, то  субнормальна в
субнормальна в  [8].
[8].
Но фактически эти два результата были получены как обобщения следующего наблюдения: каждая перестановочная подгруппа конечной группы является субнормальной [7].
Разрабатывая этот результат Ito и Szep доказали, что для каждой перестановочной подгруппы  конечной группы
конечной группы  ,
,  – нильпотентна [9].
– нильпотентна [9].
Немного позже было доказано, что при таких условиях,  [18].
[18].
При некоторых естественных условиях мы встречаемся с ситуацией, когда некоторые подгруппы  и
и  группы
группы  неперестановочны, но существует подгруппа
неперестановочны, но существует подгруппа  такая, что
такая, что  для некоторого
для некоторого  .
.
Основываясь на этом наблюдении мы дадим следующие определения.
Определение 1 Пусть  ,
,  – подгруппы группы
– подгруппы группы  и
и  . Тогда мы говорим, что:
. Тогда мы говорим, что:
(1)  является
является  -перестановочной с
-перестановочной с  , если для некоторого
, если для некоторого  имеем
имеем  .
.
(2)  является наследственно
является наследственно  -перестановочной с
-перестановочной с 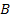 , если
, если  для некоторого
для некоторого  .
.
Заметим, что  – перестановочные подгруппы также являются перестановочными подгруппами. Во втором приведённом случае мы имеем дело с
– перестановочные подгруппы также являются перестановочными подгруппами. Во втором приведённом случае мы имеем дело с  -перестановочными подгруппами, которые были исследованы и использованы в [].
-перестановочными подгруппами, которые были исследованы и использованы в [].
Определение 2 Подгруппа  группы
группы  называется (наследственно)
называется (наследственно)  -перестановочной, если она (наследственно) перестановочна со всеми подгруппами группы
-перестановочной, если она (наследственно) перестановочна со всеми подгруппами группы 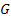 .
.
Целью данной работы является изложение некоторых известных разделов теории перестановочных подгрупп, изучение и применение некоторых свойств  -перестановочных подгрупп.
-перестановочных подгрупп.
 2020-01-15
2020-01-15 186
186







