Перший алгоритм методу

Нехай потрібно вирішити систему лінійних алгебраїчних рівнянь

(1)

с позитивно певною матрицею A порядку n.

Розглянемо функціонала

, (2)

багаточлен, що представляє, другого порядку відносно _x1, _x2…, x_n,… Позначимо через рішення системи (1), тобто . У силу симетричності й позитивної визначеності матриці, маємо:

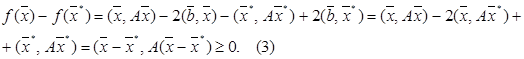
При цьому знак рівності можливий лише при . Таким чином, задача рішення рівняння (1) зводиться до задачі відшукання вектора , що обертає в мінімум функціонал (2).

Для відшукання такого вектора застосуємо наступний метод.

Нехай – довільний початковий вектор, а

(4)

– вектор не в'язань системи. Покажемо, що вектор не в'язань має напрямок нормалі до поверхні в крапці . Справді, напрямок нормалі збігається з напрямком найшвидшої зміни функції в крапці . Це напрямок ми знайдемо, якщо знайдемо серед векторів , для яких 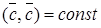, такий вектор, що

має найбільше значення. Але

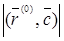Але серед векторів постійний довжини досягає максимального значення, якщо має напрямок вектора або йому протилежне. Твердження доведене. Будемо рухатися із крапки в напрямку вектора доти, поки функція досягає мінімального значення. Це буде при 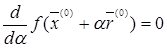, тобто при

. (5)

Вектор

(6)

і приймаємо за нове наближення до рішення.

У методі сполучених градієнтів наступне наближення перебуває так. Через крапку 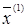проведемо гіперплощину (n-1) – го виміру

(7)

і через позначимо нове не в'язання системи

. (8)

Вектор спрямований по нормалі до поверхні в крапці 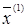, а вектор паралельний дотичної площини в цій крапці. Тому

. (9)

Гіперплощина (7) проходить через крапку , тому що

При кожному вектор паралельний деякої нормальної площини до поверхні в крапці 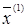. Знайдемо серед них той, котрий лежить у гіперплощині (7), тобто ортогональний к. З умови ортогональності маємо:

або

. (10)

Вектор

(11)

має напрямок нормалі до перетину поверхні гіперплощини (7) у крапці . Будемо рухатися із крапки в напрямку вектора доти, поки функція досягне мінімуму. Це буде при

. (12)

Вектор

приймемо за нове наближення до рішення системи. Вектор не в'язань

(13)

має напрямок нормалі до поверхні 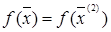в крапці . Покажемо, що він буде ортогональний до і . Справді, використовуючи (9), (11), (12), (13), маємо:

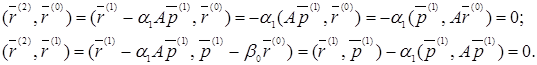
Розглянемо гіперплощину (n-2) – х вимірів

, (14)

минаючу через крапку . Ця гіперплощина містить і 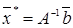, тому що ми раніше бачили, що , а

Вектор при кожному 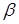паралельний гіперплощини (7), тому що

Підберемо 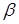так, щоб він був паралельний і гіперплощини (14), тобто зажадаємо ортогональності до вектора . Будемо мати:

або

(15)

Вектор

(16)

буде мати напрямок нормалі до перетину поверхні гіперплощиною (14) у крапці . Із крапки змістимося в напрямку цього вектора так, щоб функція досягла мінімального значення. Це буде при

, (17)

(18)

приймемо за нове наближення к. Новий вектор не в'язань буде:

. (19)

Продовжуючи процес, одержимо послідовності векторів , , , обумовлені рекурентними співвідношеннями:

(20)

Для цих векторів мають місце наступні співвідношення:

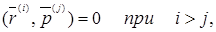(21)

(22)

Справді, у силу самої побудови при i (j

Далі, при i>j

Якщо i=j+1, то права частина дорівнює нулю, у силу визначення , якщо ж i>j+1, те , по доведеному, і

Продовжуючи зниження індексу у вектора 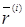, через кілька кроків прийдемо до скалярного добутку (по визначенню ). Таким чином, співвідношення (21) доведені. Для доказу (22), у силу рівноправності індексів i і j, припустимо, що i>j. Тоді

Тому що в n-мірному векторному простори не може бути більше n взаємно ортогональних векторів, то на деякому кроці одержимо , тобто буде рішенням системи (1).