Определить оценки математического ожидания и дисперсии

Задача 6

В серии из 30 выстрелов наблюдалось 8 попаданий в мишень. Найти доверительный интервал для вероятности попадания в мишень при надежности .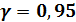

Решение

По условию n = 30 и k= 8, следовательно, m = 8/30. Далее по таблице для функции Лапласа находим t_g = 2,045. Подставляя полученные значения в формулу

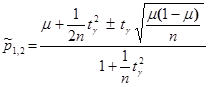
 имеем:

;

.

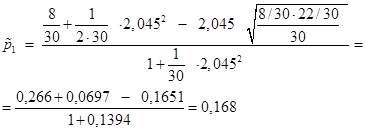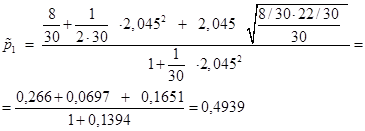Таким образом с вероятностью ³ 0,95 выполняется неравенство

0,168 < p < 0,4939.

Задача 7

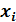
	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3
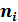
	6	9	26	25	30	26	21	24	20	8	5

Задание 1. Построить статистический ряд распределения.

Построить эмпирическую функцию распределения

Определить оценки математического ожидания и дисперсии

4. Сформулировать гипотезу о законе распределения генеральной совокупности и проверить эту гипотезу с помощью критерия 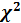, взяв .

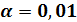Решение

Задание 1. Построить статистический ряд распределения

Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы 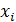, а вторая - их частоты 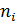(относительные частоты).

	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3	Сумма
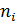
	6	9	26	25	30	26	21	24	20	8	5	200
fi	0,03	0,045	0,13	0,125	0,15	0,13	0,105	0,12	0,1	0,04	0,025	1

Построить эмпирическую функцию распределения

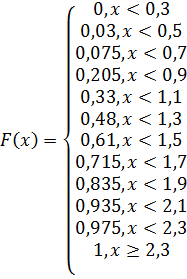
Определить оценки математического ожидания и дисперсии

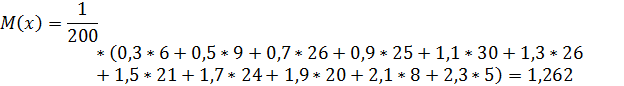
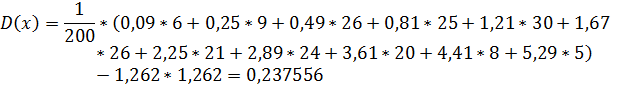
4. Сформулировать гипотезу о законе распределения генеральной совокупности и проверить эту гипотезу с помощью критерия 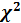, взяв .

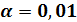1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.

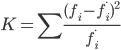
где f*_i - теоретические частоты:

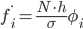
Вычислим теоретические частоты, учитывая, что:

N = 200, h=0.2 (ширина интервала), σ = 0.49, x_ср = 1.3

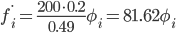
i	xi	ui	φi	fi*
1	0.3	-1.963	0,0573	4.677
2	0.5	-1.5549	0,1182	9.648
3	0.7	-1.1468	0,2059	16.806
4	0.9	-0.7387	0,3034	24.764
5	1.1	-0.3306	0,3765	30.731
6	1.3	0.07754	0,3977	32.462
7	1.5	0.4857	0,3538	28.878
8	1.7	0.8938	0,2661	21.72
9	1.9	1.3019	0,1691	13.802
10	2.1	1.71	0,0909	7.42
11	2.3	2.1181	0,0422	3.444

Сравним эмпирические и теоретические частоты. Составим расчетную таблицу, из которой найдем наблюдаемое значение критерия:

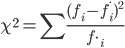
i	fi	f*i	fi-fi*	(fi-fi*)2	(fi-fi*)2/fi*
1	6	4.677	-1.323	1.7503	0.374
2	9	9.6479	0.6479	0.4197	0.0435
3	26	16.8062	-9.1938	84.5259	5.029
4	25	24.7645	-0.2355	0.05548	0.00224
5	30	30.7311	0.7311	0.5345	0.0174
6	26	32.4615	6.4615	41.7513	1.286
7	21	28.8783	7.8783	62.0671	2.149
8	24	21.7199	-2.2801	5.1988	0.239
9	20	13.8025	-6.1975	38.4093	2.783
10	8	7.4195	-0.5805	0.3369	0.0454
11	5	3.4445	-1.5555	2.4196	0.702
∑	200	200			12.672

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение K_набл, тем сильнее довод против основной гипотезы.

Поэтому критическая область для этой статистики всегда правосторонняя: [K_kp;+∞).

Её границу K_kp = χ²(k-r-1;α) находим по таблицам распределения χ² и заданным значениям σ, k = 11, r=2 (параметры x_cp и σ оценены по выборке).

Kkp(0.01;8) = 20.09024; Kнабл = 12.67

Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.