2020-01-15
159
· шаг 0. Определение начального базиса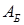 
и соответствующей ему начальной угловой точки (базисного плана) 
.
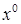· шаг 1. Проверка текущего базисного плана на оптимальность. Если критерий оптимальности выполнен,топлан оптимален и решение закончено. Иначе переход на шаг 2.
· шаг 2. Нахождение переменной, вводимой в состав базисных. (Из условия увеличения целевой функции).
· шаг 3. Нахождение переменной, исключаемой из состава базисных переменных (Из условия сохранения ограничений задачи).
· шаг 4. Нахождение координат нового базисного плана (смежной угловой точки). Переход на шаг 1.
Повторяющиеся шаги 1–4 образуют одну итерацию симплекс-метода.
Из этой схемы следует, что во-первых, для начала работы симплекс-метода надо иметь какую-то угловую точку – начальный базисный план, а во-вторых, надо уметь исследовать текущую угловую точку на оптимальность, не вычисляя всех смежных вершин. Эти проблемы легко решаются, если каноническая задача ЛП имеет некий специальный вид.
Определение. Будем говорить, что каноническая задача ЛП имеет "предпочтительный вид", если
|
|
|
1. правые части уравнений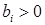 
, 
.
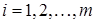2. матрица условий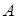 
содержит единичную подматрицу размера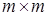 
.
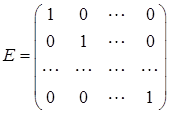Другими словами, в любом уравнении есть переменная с коэффициентом равным единице, отсутствующая в остальных уравнениях. Первое условие не является обременительным, так как в случае отрицательной правой части некоторого уравнения, достаточно умножить его на (–1). В задаче предпочтительного вида начальный базисный план находится очень просто.
Пример 2.1.
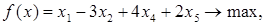
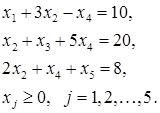
Матрица условий A и вектор правых частей ограничений b имеют вид
, 
,
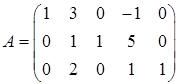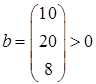а целевой вектор с = (1, -3, 0, 4, 2).
Сразу очевидна одна базисная матрица: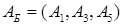 
с единичными векторами условий.
Следовательно, выбирая в качестве базисных переменных x1, x3, x5, и полагая в системе уравнений x2 = x4 = 0 (небазисные переменные), немедленно находим x1 = 10, x3 = 20, x5 = 8, так что начальный базисный план x0 = (10, 0, 20, 0, 8).Видим, что значения базисных переменных равны правым частям ограничений. Из этого понятно требование положительности правых частей bi.
В дальнейшем, базисные переменные будем объединять в вектор xБ.
Таким образом, в канонической задаче предпочтительного вида в качестве начальной базисной матрицы берется единичная подматрица AБ = E, а соответствующие ей базисные переменные равны правым частям ограничений:
xБ = b.
Для базисного плана такого вида может быть сформулирован достаточно простой для проверки критерий оптимальности. Введем величины
∆j = < сБ, Aj > – cj, j = 1,...,n, (2.1)
где сБ – вектор из коэффициентов целевой функции при базисных переменных xБ, Aj – j- йстолбец матрицы условий, cj – j- й коэффициент целевой функции. Разности ∆j называются симплексными разностями или симплексными оценками.
|
|
|
Критерий оптимальности базисного плана. Если для базисного плана с единичной базисной матрицей все симплексные оценки неотрицательны, то этот план оптимален.
Применим данный критерий для проверки на оптимальность базисного плана x0 = (10, 0, 20, 0, 8) из примера 2.1.
Так как в этом плане вектор базисных переменных xБ =(x1, x3, x5), то сБ = (c1, c3, c5) = (1, 0, 2).
.
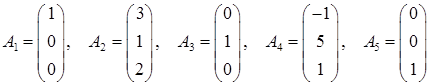Следовательно,
∆1 = < сБ, A1 > – c1 =1∙1 + 0∙0 + 2∙0 – 1= 0,
∆2 = < сБ, A2 > – c2 =1∙3 + 0∙1 + 2∙2 – (-3) = 10,
∆3 = < сБ, A3 > – c3 =1∙0 + 0∙1 + 2∙0 – 0= 0,
∆4 = < сБ, A4 > – c4 =1∙(-1) + 0∙5 + 2∙1 – 4= -3,
∆5 = < сБ, A5 > – c5 =1∙0 + 0∙0 + 2∙1 – 2= 0.
Так как оценка ∆4 < 0, то базисный план x0 не оптимален. Заметим, что симплексные оценки, соответствующие базисным переменным, всегда равны нулю, так что достаточно проверять только небазисные оценки.
