2020-01-14
100
Нормальное распределение зависит от двух параметров: средней арифметической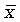 
и среднего квадратического отклонения 
. Его кривая выражается уравнением
где у - ордината кривой нормального распределения; 
- стандартизованные отклонения; е и π - математические постоянные; x - варианты вариационного ряда; 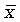- их средняя величина; - cреднее квадратическое отклонение.
Если нужно получить теоретические частоты f' при выравнивании вариационного ряда по кривой нормального распределения, то можно воспользоваться формулой
где 
- сумма всех эмпирических частот вариационного ряда; h - величина интервала в группах; - среднее квадратическое отклонение; - нормированное отклонение вариантов от средней арифметической; все остальные величины легко вычисляются по специальным таблицам.
Вычисление критерия согласия Пирсона.
Наиболее распространенным является критерий согласия К. Пирсона 
, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:
Вычисленное значение критерия 
необходимо сравнить с табличным (критическим) значением 
. Табличное значение определяется по специальной таблице, оно зависит от принятой вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число групп в ряду распределения для нормального распределения). При расчете критерия согласия Пирсона должно соблюдаться следующее условие: достаточно большим должно быть число наблюдений (n >=50), при этом если в некоторых интервалах теоретические частоты < 5, то интервалы объединяют для условия > 5.
Если 
, то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.
