Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов
u и
v равно
u · v = | u | · | v | · cos j, где
j — угол между векторами. Если векторы ортогональны, их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом умножения (пример на рис.11). Для обозначения скалярного произведения пользователь также может выбирать представление оператора умножения.
|
| | | Рис.11 Скалярное произведение векторов
| |
Никогда не применяйте для обозначения скалярного произведения символ который является общеупотребительным символом векторного произведения.
С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения см. в листинге на рис.12.
|
| | | Рис.12 Особенности скалярного произведения векторов
| |
Векторное произведение
| Рис.13 Векторное произведение векторов
| |
Векторное произведение (cross product) двух векторов
u и
v с углом a между ними равно вектору с модулем
| u | · | v | · sin a, направленным перпендикулярно носкости векторов
u и
v. Обозначают векторное произведение символом
х, который можно ввести нажатием кнопки
Cross Product (Векторное произвение) в панели
Matrix (Матрица) или сочетанием клавиш
<Ctrl>+<8>. Пример приведен на рис.13.
Задание 1.
Вычислите матрицу 2*A*B-3*C*D, где:
Ответ:



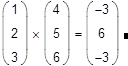
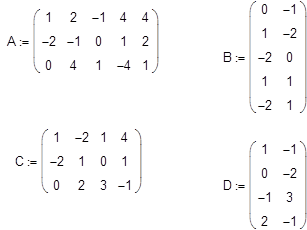

 2020-01-14
2020-01-14 126
126







