Существование линейно независимых векторов среди собственных, отвечающих различным собственным числам λ1, λ2, …, λn, определяется следующей теоремой.
Собственные векторы x1, x2, …, xn оператора, отвечающие различным собственным значениям λ1, λ2, …, λn, линейно независимы.
На n линейно независимых собственных векторах можно построить базис n-мерного линейного векторного пространства.
Замечание. Определитель матрицы P – λE (соответственно характеристический многочлен) не зависит от выбора базиса.
|P’ – λE| =|T-1PT – λE| =|T-1PT- λ T-1 E T | =|T-1P- λ E T | =|T-1||P- λ E T | |T|=|P- λ E T |
Следовательно, при переходе к новому базису собственные числа сохраняются.
Пример. Найти собственные значения и собственные векторы линейного оператора 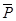 , заданного матрицей P=
, заданного матрицей P= 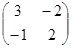 в пространстве R2.
в пространстве R2.
Решение. Составим характеристическое уравнение:
|P – λ·E| = 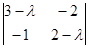 = λ2-5 λ+4=0
= λ2-5 λ+4=0
Из квадратного уравнения найдем собственные значения линейного оператора λ1=1, λ2=4. Чтобы найти собственные векторы, решим матричные уравнения:
(P – λ1 E) X=0 и (P – λ2 E) X=0
В развернутом виде
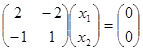 и
и 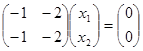
Соответствующие однородные системы:
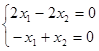
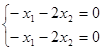
Общие решения систем:
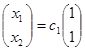 и
и 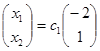 , где с1, с2 є R
, где с1, с2 є R
Таким образом, множество собственных векторов, отвечающих собственным значениям λ1=1, λ2=4, имеет вид 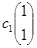 ;
; 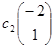 , где с1, с2 є R. Векторы a1=(1, 1), a2=(-2, 1), например, являются линейно независимыми. Они могут быть приняты в качестве нового базиса в пространстве R2.
, где с1, с2 є R. Векторы a1=(1, 1), a2=(-2, 1), например, являются линейно независимыми. Они могут быть приняты в качестве нового базиса в пространстве R2.
Пусть e1, e2, …, en – собственные векторы линейного оператора 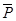 в пространстве Rn, которые примем в качестве базиса. Тогда разложение векторов
в пространстве Rn, которые примем в качестве базиса. Тогда разложение векторов 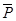 (e1),
(e1), 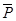 (e2), …,
(e2), …, 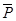 (en) по базису e1, e2, …, en примет вид
(en) по базису e1, e2, …, en примет вид
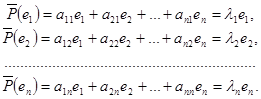
Отсюда следует, что aij= λi, если i=j и aij=0, если i≠j. Поэтому в базисе, составленном из собственных векторов, матрица оператора будет иметь диагональный вид:
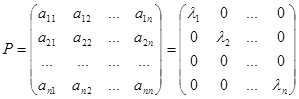
Симметричный оператор
Определение. Линейный оператор 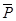 в евклидовом пространстве Rn называется симметричным, если для любых векторов x и y из пространства Rn выполняется равенство
в евклидовом пространстве Rn называется симметричным, если для любых векторов x и y из пространства Rn выполняется равенство
(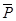 (x), y)= (x,
(x), y)= (x, 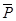 (y))
(y))
 2020-01-14
2020-01-14 173
173








