Для того чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была симметрична

Рассмотрим для простоты евклидово пространство R². Пусть в ортобазисе e₁, e₂ заданы векторы x=(x₁, x₂), y=(y₁, y₂). Линейные операторы 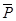₁ и 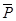₂ определены своими матрицам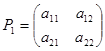и:

и .

Вычислим векторы ₁(x) и ₂(y):

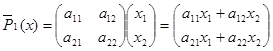Найдем скалярные произведения ( (x), y) и (x, (y)):

( (x), y)=(a₁₁x₁+a₁₂x₂) y₁+(a₂₁x₁+a₂₂x₂) y₂=a₁₁y₁x₁+a₁₂y₁x₂+a₂₁y₂x₁+a₂₂y₂x₂,

(x, (y))= (b₁₁y₁+b₁₂y₂) x₁+(b₂₁y₁+b₂₂y₂) x₂=b₁₁x₁y₁+b₁₂x₁y₂+b₂₁x₂y₁+b₂₂x₂y₂.

Найдем разность скалярных произведений:

( (x), y) – (x, (y)) = (a₁₁-b₁₁) x₁y₁+(a₂₁-b₁₂) x₁y₂+(a₁₂-b₂₁) x₂y₁+(a₂₂-b₂₂) x₂y₂.

Если для любых векторов x и y из пространства R² равенство

( (x), y) – (x, (y))=0 (3)

Выполнено (необходимость), то верна система

a₁₁=b₁₁,

a₂₁=b₁₂,

a₁₂=b₂₁, (4)

a₂₂=b₂₂,

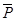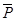и обратно: если условия (4) соблюдены для любых векторов x и y, то равенство (3) выполнено (достаточность). Система равенств (4) означает, что ₁= ₂= .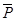

Ортогональность собственных векторов

Собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимо ортогональны.

Пусть x и y – собственные векторы оператора , соответствующие собственным числам λ₁ и λ₂, причем λ₁ ≠ λ₂. По определению симметричного оператора:

( (x), y)= (x, (y))

Подставив сюда правые части равенства ( (x))= λ₁x, (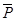 (y))= λ₁y, получим

(λ₁x, y)=(x, λ₂y). Вынесем числа λ₁ и λ₂, за знак скалярного произведения, перенесем слагаемые влево и разложим на множители: (λ₁ – λ₂) (x, y)=0

Поскольку λ₁ ≠ λ₂, получаем (x, y)=0, что и означает взаимную ортогональность векторов x и y.

Отметим другие важные свойства симметричного оператора.

1) Характеристическое уравнение симметричного оператора имеет только действительные корни.

2) Если в евклидовом пространстве Rⁿ задан симметричный оператор 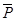, то в Rⁿ существует ортонормированный базис e₁, e₂, …, e_n, составленный из собственных векторов .