Глава 1. Теория уравнений с двумя переменными в целых числах.
1. Историческая справка _______________________________________5
1.1 Теоремы о числе решений линейных диофантовых уравнений___6
1.2 Алгоритм решения уравнения в целых числах_________________ 6
1.3 Способы решения уравнений_______________________________ 7
Глава 2. Применение способов решения уравнений.
1. Решение задач_____________________________________________ 8
2.1 Решение задач с помощью алгоритма Евклида________________ 8
2.2 Способ перебора вариантов________________________________ 9
2.3 Метод разложения на множители___________________________ 9
2.4 Метод остатков__________________________________________ 12
2. Задачи экзаменационного уровня___________________________ 13
Заключение________________________________________________ 16
Список используемой литературы_____________________________ 17
«Кто управляет числами,
Тот управляет миром»
Пифагор.
Введение.
Анализ ситуации: Диофантовы уравнения это актуальная в наше время тема, т. к. решение уравнений, неравенств, задач, сводящихся к решению уравнений в целых числах с помощью оценок для переменных, встречается в различных математических сборниках и сборниках ЕГЭ.
Изучив разные способы решения квадратного уравнения с одной переменной на уроках, нам было интересно разобраться, а как решаются уравнения с двумя переменными. Такие задания встречаются на олимпиадах и в материалах ЕГЭ.
В этом учебном году одиннадцатиклассникам предстоит сдавать Единый государственный экзамен по математике, где КИМы составлены по новой структуре. Нет части «А», но добавлены задания в часть «В» и часть «С». Составители объясняют добавление С6 тем, что для поступления в технический ВУЗ нужно уметь решать задания такого высокого уровня сложности.
Проблема: Решая примерные варианты заданий ЕГЭ, мы заметили, что чаще всего встречаются в С6 задания на решение уравнений первой и второй степени в целых числах. Но мы не знаем способы решения таких уравнений. В связи с этим возникла необходимость изучить теорию таких уравнений и алгоритм их решения.
Цель: Освоить способ решения уравнений с двумя неизвестными первой и второй степени в целых числах.
Задачи: 1) Изучить учебную и справочную литературу;
2) Собрать теоретический материал по способам решения уравнений;
3) Разобрать алгоритм решения уравнений данного вида;
4) Описать способ решения.
5) Рассмотреть ряд примеров с применением данного приема.
6) Решить уравнения с двумя переменными в целых числах из
материалов ЕГЭ-2010 С6.
Объект исследования: Решение уравнений
Предмет исследования: Уравнения с двумя переменными в целых числах.
Гипотеза: Данная тема имеет большое прикладное значение. В школьном курсе математики подробно изучаются уравнения с одной переменной и различные способы их решения. Потребности учебного процесса требуют, чтобы ученики знали и умели решать простейшие уравнения с двумя переменными. Поэтому повышенное внимание к этой теме не только оправдано, но и является актуальной в школьном курсе математики.
Данная работа может быть использована для изучения данной темы на факультативных занятиях учениками, при подготовке к выпускным и вступительным экзаменам. Мы надеемся, что наш материал поможет старшеклассникам научиться решать уравнения такого вида.
Глава 1. Теория уравнений с двумя переменными в целых числах.
1. Историческая справка.
Диофант и история диофантовых уравнений.
Решение уравнений в целых числах является одной из древнейших математических задач. Наибольшего расцвета эта область математики достигла в Древней Греции. Основным источником, дошедшим до нашего времени, является произведение Диофанта – «Арифметика». Диофант суммировал и расширил накопленный до него опыт решения неопределенных уравнений в целых числах.
История сохранила нам мало черт биографии замечательного александрийского ученого-алгебраиста Диофанта. По некоторым данным Диофант жил до 364 года н.э. Достоверно известно лишь своеобразное жизнеописание Диофанта, которое по преданию было высечено на его надгробии и представляло задачу-головоломку:
«Бог ниспослал ему быть мальчиком шестую часть жизни; добавив к сему двенадцатую часть, Он покрыл его щеки пушком; после седьмой части Он зажег ему свет супружества и через пять лет после вступления в брак даровал ему сына. Увы! Несчастный поздний ребенок, достигнув меры половины полной жизни отца, он был унесен безжалостным роком. Через четыре года, утешая постигшее его горе наукой о числах, он [Диофант] завершил свою жизнь» (примерно 84 года).
Эта головоломка служит примером тех задач, которые решал Диофант. Он специализировался на решении задач в целых числах. Такие задачи в настоящее время известны под названием диофантовых.
Наиболее известной, решенной Диофантом, является задача «о разложении на два квадрата». Ее эквивалентом является известная всем теорема Пифагора. Эта теорема была известна в Вавилонии, возможно ее знали и в Древнем Египте, но впервые она была доказана, в пифагорейской школе. Так называлась группа интересующихся математикой философов по имени основателя школы Пифагора (ок. 580-500г. до н.э.)
Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.
Теоремы о числе решений линейного диофантового уравнения.
Приведем здесь формулировки теорем, на основании которых может быть составлен алгоритм решения неопределенных уравнений первой степени от двух переменных в целых числах.
Теорема 1. Если в уравнении 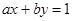 ,
, 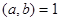 , то уравнение имеет, по крайней мере, одно решение.
, то уравнение имеет, по крайней мере, одно решение.
Теорема 2. Если в уравнении 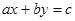 ,
, 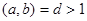 и с не делится на
и с не делится на 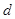 , то уравнение целых решений не имеет.
, то уравнение целых решений не имеет.
Теорема 3. Если в уравнении 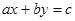 ,
,  и
и 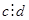 , то оно равносильно уравнению
, то оно равносильно уравнению 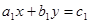 , в котором
, в котором 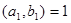 .
.
Теорема 4. Если в уравнении 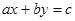 ,
, 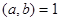 , то все целые решения этого уравнения заключены в формулах:
, то все целые решения этого уравнения заключены в формулах:
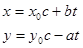
где х0, у0 – целое решение уравнения 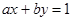 ,
, 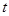 - любое целое число.
- любое целое число.
1.2. Алгоритм решения уравнения в целых числах.
Сформулированные теоремы позволяют составить следующий алгоритм решения в целых числах уравнения вида 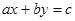 .
.
1. Найти наибольший общий делитель чисел a и b,
если 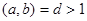 и с не делится на
и с не делится на  , то уравнение целых решений не имеет;
, то уравнение целых решений не имеет;
если 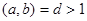 и
и 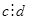 , то
, то
2. Разделить почленно уравнение 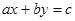 на
на  , получив при этом уравнение
, получив при этом уравнение 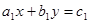 , в котором
, в котором 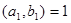 .
.
3. Найти целое решение (х0, у0) уравнения 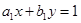 путем представления 1 как линейной комбинации чисел
путем представления 1 как линейной комбинации чисел 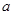 и
и 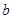 ;
;
4. Составить общую формулу целых решений данного уравнения
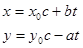
где х0, у0 – целое решение уравнения 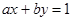 ,
, 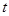 - любое целое число.
- любое целое число.
 2020-01-14
2020-01-14 209
209







