Для деления в общем случае используется алгоритм Д. Кнута. Будем делить «в столбик» число 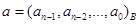 на число
на число 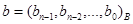 .Найдем такое частное
.Найдем такое частное 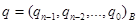 и остаток
и остаток 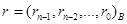 , что
, что 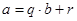 .
.
При делении на каждом шаге находим частное 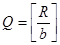 от деления некоторого (n+1)-разрядного числа
от деления некоторого (n+1)-разрядного числа 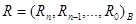 на b, где О < R/b< В. Неравенство R/b < В эквивалентно неравенству R/B<b, откуда b:
на b, где О < R/b< В. Неравенство R/b < В эквивалентно неравенству R/B<b, откуда b:
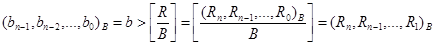
Полагая R = R - Qb, получаем 0 < R < b.
Для определения числа Q будем использовать аппроксимацию
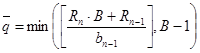 [1]
[1]
При 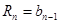 получаем
получаем 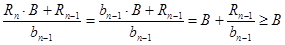
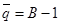 , то есть определение наименьшего из двух чисел в выражении
, то есть определение наименьшего из двух чисел в выражении
(1) сводится к проверке равенства 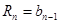 .
.
Теорема 1.
Пусть 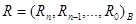 ,
, 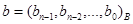 , если
, если 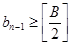 то значение
то значение 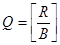 удовлетворяет неравенству
удовлетворяет неравенству 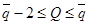 , где q определяется из соотношения (1.1).
, где q определяется из соотношения (1.1).
Алгоритм деления с остатком. Чтобы старший разряд делителя удовлетворял условию теоремы 1.1, числа а и b нужно умножить на некоторое целое число d>0, такое что 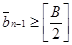 где.
где.
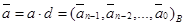 ,
, 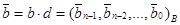
Частное при этом не изменяется: 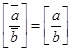 . Число разрядов
. Число разрядов 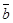 недолжно превышать число разрядов b, число разрядов в
недолжно превышать число разрядов b, число разрядов в 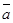 может быть на единицу больше, чем в а (если это не так, полагаем ат+п = 0).Выбираем d равным степени двойки, так как умножение на d в этом случае выполняется сдвигом.
может быть на единицу больше, чем в а (если это не так, полагаем ат+п = 0).Выбираем d равным степени двойки, так как умножение на d в этом случае выполняется сдвигом.
Алгоритм 4. Деление «в столбик», [Молдовян Н.А. и др., 2004].
Вход. Неотрицательные целые числа 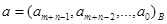 ,
, 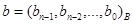 ;
;
Выход. Целые числа 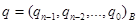 ,
, 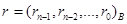 , такие, что
, такие, что 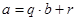 ,
, 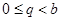 .
.
1. Определить такое целое число d>0, что 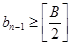 , где
, где 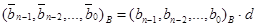
2. Положить 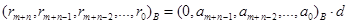 .
.
3. Для i = m + n,m + n - 1,..., n выполнить следующие действия
3.1. Если ri=bn-1, то положить 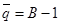 ; в противном случае найти
; в противном случае найти 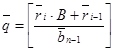 где
где 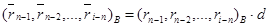 .
.
3.2. Пока 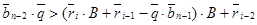 полагать
полагать 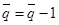
3.3. При 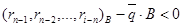 положить
положить 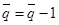 .
.
3.4. Вычислить 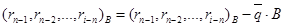 и
и 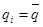 .
.
4. Результат: 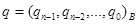 ,
, 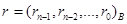
Сложность алгоритма деления «в столбик» равна О(mn).
Реализованы две функции целочисленное деление и вычисление остатка.
Основной код функций:
for(i=64;i>=0;i--){
ai=i+1;
if(a[i]!=0)break;
}
for(i=32;i>=0;i--){
n=i+1;
if(b[i]!=0)break;
}
m=ai-n;
//printf("b = %x ",b[n-1]);
d=1;
if(b[n-1]<128){
for(i=2;i<=7;i++){
d*=2;
if((b[n-1]*d)>=128) break;
}
}//оценить d шаг 1
mult(b,d,bt);//шаг 1 b~=b*d
for(i=0;i<=63;i++){r[i]=a[i];}//шаг 2
for(i=m+n;i>=n;i--){//шаг 3
s=0;
for(k=i-n;k<=i;k++){
t=r[k]*d+s;
rt[k]=t;
s=t>>8;
}// шаг 3.1 r~=r*d
if(rt[i]==bt[n-1]) qt=255;
else qt=((rt[i]*256+rt[i-1])/bt[n-1]);// шаг 3.1 r~=r*d
while((bt[n-2]*qt)>((rt[i]*256+rt[i-1]-qt*bt[n-1])*256+rt[i-2])){
qt-=1;
}// шаг 3.2
mult(b,qt,bqt); 
for(k=i;k>=i-n;k--){
if(r[k]<bqt[k-m]){
qt-=1;
break;
}
if(rt[k]>bqt[k-m])break;
}// шаг 3.3
mult(b,qt,bqt);
s=0;
for(k=i-n;k<=i;k++){
t=r[k]-bqt[k-m]+s;
r[k]=t;
s=t>>8;
}
c[i-n]=qt;
m-=1;
}
В итоге: r - остаток от деления,c – целое от деления.
Тест Рабина—Миллера
На сегодняшний день для проверки чисел на простоту чаще всего используется тест Рабина-Миллера, основанный на следующем наблюдении. Пусть число п нечетное и 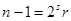 , где r — нечетное. Если п простое, то для любого а ≥ 2, взаимно простого с п, выполняется условие теоремы Ферма (аr = 1 (mod n)). Разложим число
, где r — нечетное. Если п простое, то для любого а ≥ 2, взаимно простого с п, выполняется условие теоремы Ферма (аr = 1 (mod n)). Разложим число 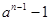 на множители:
на множители:
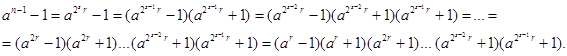
Тогда в последнем произведении хотя бы одна из скобок делится на п, то есть либо аr= 1(mod п), либо среди чисел а, аr,..., 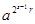 найдется сравнимое с -1 по модулю п.
найдется сравнимое с -1 по модулю п.
Обращение этого свойства лежит в основе теста Рабина-Миллера.
Алгоритм 5. Тест Рабина-Миллера, [Молдовян Н.А. и др., 2004].
Вход. Нечетное целое число п ≥ 5.
Выход. «Число п, вероятно, простое» шли «Число п составное».
1. Представить п - 1 в виде 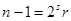 , где число r нечетное.
, где число r нечетное.
2. Выбрать случайное целое число а, 2 ≤ а ≤ п - 2.
3. Вычислить 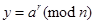 .
.
4. При 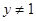 и
и 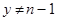 выполнить следующие действия.
выполнить следующие действия.
4.1. Положить j = 1.
4.2. Если j ≤ s – 1 и 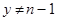 .
.
4.2.1. Положить y=y2 (mod n)
4.2.2. При у = 1 результат: «Числю п составное».
4.2.3. Положить j=j+1.
4.3. При 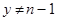 результат: «Число п составное».
результат: «Число п составное».
5. Результат: «Число п, вероятно, простое».
В результате выполнения теста для простого числа п в последовательности a (mod n), a2r(mod n),..., 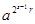 (mod n) обязательно перед 1 должна появиться -1 (или, что то же самое, п - 1 (mod n)). Это означает, что для простого числа п единственными решениями сравнения y2 = 1 (mod n)являются у = ±1 (mod n). Если число n составное и имеет k> 1 различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует 2k решений сравнения у2 = 1 (mod n). Действительно, для любого простого делителя pi числа п существует два решения указанного сравнения: у = ± 1(mod рi). Поэтому k таких сравнений дают 2k наборов решений по модулям pi, содержащих элементы ± 1.
(mod n) обязательно перед 1 должна появиться -1 (или, что то же самое, п - 1 (mod n)). Это означает, что для простого числа п единственными решениями сравнения y2 = 1 (mod n)являются у = ±1 (mod n). Если число n составное и имеет k> 1 различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует 2k решений сравнения у2 = 1 (mod n). Действительно, для любого простого делителя pi числа п существует два решения указанного сравнения: у = ± 1(mod рi). Поэтому k таких сравнений дают 2k наборов решений по модулям pi, содержащих элементы ± 1.
Сложность алгоритма равна 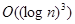
Код функции rabin (поверка на простоту):
/*mod – проверяемое значение,
st – степень числа при передаче в функцию sstep();
osn – основание при вычислении
Пр: osnst (mod mod)
*/
int rabin(){
unsigned char c[33]={0};
int i,k,g,t,q,r,x,j,fl,w;
unsigned char d[33]={0};//для р.м. р-1
srand(time(0));
for(i=0;i<=31;i++) st[i]=mod[i];
st[0]-=1;
for(i=0;i<=31;i++){
d[i]=st[i];
}
for(i=0;;i++){
q=i+1;
r=0;
for(k=31;k>=0;k--){
t=st[k]+(r<<8);
st[k]=(t>>1);
r=t%2;
}
if(int(st[0])%2==1) break;
}//находим n-1=(2^s)*q где n-простое
for(i=0;i<=6;i++){
osn[i]=rand();
}//генерируем основание
step(c);
x=comp_sp(c,d);
if(x==2){
return 1;
}
x=rav(c);
if(x==0) return 1;
j=1;
while(j<=q-1){
step2(c,c);
x=rav(c);
if(x==0) return 0;
j++;
}
x=comp_sp(c,d);
if(x!=2){
return 0;
}
return 1;
}
 2020-01-14
2020-01-14 119
119








