Пусть  - множество направлений убывания функции
- множество направлений убывания функции  в точке
в точке 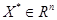 , а
, а  - множество возможных направлений относительно множества
- множество возможных направлений относительно множества  в точке
в точке  . Напомним, что вектор
. Напомним, что вектор  задаёт направление убывания функции
задаёт направление убывания функции  в точке
в точке 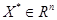 , если
, если  при всех достаточно малых
при всех достаточно малых  , и возможное направление относительно множества
, и возможное направление относительно множества  в точке
в точке  , если точка
, если точка  при всех достаточно малых
при всех достаточно малых  .
.
63. Доказать, что если  - локальное решение задачи (3) без каких-либо предположений на множество
- локальное решение задачи (3) без каких-либо предположений на множество  и функцию
и функцию  , то
, то  .
.
64. Пусть в задаче (12) множество  выпукло, а функция
выпукло, а функция  - дифференцируема в точке
- дифференцируема в точке  . Доказать, что тогда, если
. Доказать, что тогда, если  - локальное решение задачи (12), то
- локальное решение задачи (12), то
 , (13)
, (13)
если же  выпукла на
выпукла на  и выполняется (13), то
и выполняется (13), то  - глобальное решение задачи (12).
- глобальное решение задачи (12).
65. Доказать, что если  (
( - внутренняя точка множества
- внутренняя точка множества  ), то (13) эквивалентно условию
), то (13) эквивалентно условию  .
.
66. Пусть множество  имеет вид
имеет вид  , где
, где  ,
,  (если
(если  или
или  , то соответствующий знак неравенства в задании множества
, то соответствующий знак неравенства в задании множества  следует понимать как строгий). Доказать, что тогда условие (13) эквивалентно условию: для любого
следует понимать как строгий). Доказать, что тогда условие (13) эквивалентно условию: для любого 
|
|
|

67. Пусть множество  имеет вид
имеет вид  ,
,  (
( соответствует случаю
соответствует случаю  ). Доказать, что тогда (13) эквивалентно условиям:
). Доказать, что тогда (13) эквивалентно условиям:

68. Решить задачу:

69. Решить задачу:

70. Пусть  - дифференцируемая сильно выпуклая функция на
- дифференцируемая сильно выпуклая функция на  . Показать, что при любом
. Показать, что при любом  решение уравнения
решение уравнения  на
на  существует и единственно.
существует и единственно.
71. Пусть  - дифференцируемая выпуклая функция на
- дифференцируемая выпуклая функция на  . Показать, что при любом
. Показать, что при любом  решение уравнения
решение уравнения  на
на  существует и единственно.
существует и единственно.
Напомним необходимое условие оптимальности (Принцип Лагранжа) в задаче математического программирования (1).
Теорема 12 (Принцип Лагранжа)
Пусть в задаче (1) множество  - выпукло, функции
- выпукло, функции  дифференцируемы в точке
дифференцируемы в точке  , функции
, функции  непрерывно дифференцируемы в некоторой окрестности точки
непрерывно дифференцируемы в некоторой окрестности точки  . Если
. Если  - локальное решение задачи (1), то существует число
- локальное решение задачи (1), то существует число  и вектор
и вектор  не равные нулю одновременно и такие, что
не равные нулю одновременно и такие, что
 (14)
(14)
 . (15)
. (15)
Используемые здесь обозначения пояснены после формулировки задачи (1) на странице 3, а числа  , также как в классической задаче на условный экстремум, называются множителями Лагранжа.
, также как в классической задаче на условный экстремум, называются множителями Лагранжа.
Теорема 13 (Достаточное условие оптимальности)
Пусть в задаче (1) множество  выпукло, функции
выпукло, функции  выпуклы на
выпуклы на  и дифференцируемы в точке
и дифференцируемы в точке  , функции
, функции  линейны. Если при
линейны. Если при  и некотором
и некотором  выполняются условия (14), (15), то
выполняются условия (14), (15), то  - глобальное решение задачи (1).
- глобальное решение задачи (1).
Теорема 14 (Условия регулярности)
Пусть в задаче (1) множество  выпукло, функции
выпукло, функции  дифференцируемы в точке
дифференцируемы в точке  , функции
, функции  выпуклы на
выпуклы на  , функции
, функции  линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
|
|
|
1) ограничения-равенства отсутствуют ( ) и существует точка
) и существует точка  такая, что
такая, что  при всех
при всех  ;
;
2)  , функции
, функции  линейны.
линейны.
Тогда, если  - локальное решение задачи (1), то существует
- локальное решение задачи (1), то существует  такой, что при
такой, что при  будут выполнены условия (14), (15).
будут выполнены условия (14), (15).
Условие 1) теоремы называется условием регулярности Слейтера.
Теорема 15 (Теорема Куна-Таккера в дифференциальной форме)
Пусть в дополнение к условиям теоремы 14 функция  выпукла на
выпукла на  . Тогда точка
. Тогда точка  является решением задачи (1) в том и только том случае, если существует вектор
является решением задачи (1) в том и только том случае, если существует вектор  такой, что при
такой, что при  выполняются условия (14), (15).
выполняются условия (14), (15).
Пример 3.
Рассмотрим задачу:

Решение:
1. Очевидно, что данная задача - задача выпуклого программирования.
2. Условия регулярности Слейтера выполнено, следовательно, функция Лагранжа регулярная:
 .
.
3. Выпишем необходимые условия:



Пусть  , тогда
, тогда  , но данная точка не удовлетворяет ограничению задачи. Отсюда следует, что
, но данная точка не удовлетворяет ограничению задачи. Отсюда следует, что  . Система перепишется в виде:
. Система перепишется в виде:

Разрешая систему, получим:
 .
.
4. Для задачи выпуклого программирования необходимые условия оптимальности являются и достаточными (теорема 13), то есть  - глобальное решение задачи.
- глобальное решение задачи.
72. Опираясь на решение задач 65-67, конкретизировать условие (14) в случае, когда  и когда
и когда  имеет вид, указанный в задачах 66, 67.
имеет вид, указанный в задачах 66, 67.
Проекцией точки  на множество D называется точка
на множество D называется точка  , ближайшая к
, ближайшая к  среди всех точек из D. Иными словами,
среди всех точек из D. Иными словами,  является решением задачи проектирования
является решением задачи проектирования
 .
.
Заметим, что понятие проекции точки на множество используется в численных методах условной оптимизации, основанных на идее проектирования очередной точки, вырабатываемой методом решения безусловной задачи, на допустимое множество задачи с ограничениями.
Доказать следующие утверждения для произвольной точки  .
.
73. Если  - сфера, то
- сфера, то  .
.
74. Если  - координатный параллелепипед, то
- координатный параллелепипед, то

75. Если  - неотрицательный октант, то
- неотрицательный октант, то  .
.
76. Если  - гиперплоскость (
- гиперплоскость ( ), то
), то  .
.
77. Если  - полупространство (
- полупространство ( ), то
), то  .
.
78. Если  - аффинное множество, причём строки матрицы
- аффинное множество, причём строки матрицы  линейно независимы, то
линейно независимы, то  , где
, где  - транспонированная матрица,
- транспонированная матрица,  .
.
79. Решить задачу:


80. Доказать, что решением задачи выпуклого программирования


является точка  .
.
81. Показать, что других решений, кроме  , в задаче 80 нет.
, в задаче 80 нет.
82. Доказать, что решением задачи выпуклого программирования


является точка  .
.
83. Показать, что других решений, кроме  , в задаче 82 нет.
, в задаче 82 нет.
В задачах 84-88  .
.
84. Используя необходимые условия оптимальности (14), (15), разработать численный метод отыскания решения задачи


Решить задачи:
85. 

 - положительные числа,
- положительные числа,  .
.
86. 

 - произвольные числа,
- произвольные числа,  .
.
87. 

88. 

89. 

90. 

91. 

92. 

93. 

94. Доказать, что если  ,
,  - положительные числа, причём
- положительные числа, причём  , то
, то  .
.
Пусть
 ,
,

 (17)
(17)
95. Показать, что если  дифференцируемы в точке
дифференцируемы в точке 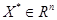 и
и  - локальное решение задачи (17), то существуют числа
- локальное решение задачи (17), то существуют числа  , такие, что
, такие, что
 .
.
Предполагая, что в задаче (1)  , обозначим через
, обозначим через  точную нижнюю грань целевой функции задачи (1) на её допустимом множестве:
точную нижнюю грань целевой функции задачи (1) на её допустимом множестве:  . Вектор
. Вектор  называется вектором Куна-Таккера задачи (1), если
называется вектором Куна-Таккера задачи (1), если  при всех
при всех  .
.
Двойственной к задаче (1) называется задача
 (18)
(18)
 ,
,  .
.
При этом задача (1) называется прямой. Предполагая, что  , обозначим через
, обозначим через  .
.
96. Показать, что в задаче (18) множество  выпукло, а функция
выпукло, а функция  вогнута на
вогнута на  .
.
97. Показать, что для любых  и
и  справедливо неравенство
справедливо неравенство  . Если
. Если  ,
,  , то
, то  .
.
Теорема 16 (Теорема существования вектора Куна-Таккера)
Пусть в задаче (1) множество  выпукло, функции
выпукло, функции  выпуклы на
выпуклы на  , функции
, функции  линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
|
|
|
1) ограничения равенства отсутствуют ( ) и существует точка
) и существует точка  такая, что
такая, что  ;
;
2)  , функции
, функции  линейны, множество
линейны, множество  .
.
Тогда вектор Куна-Таккера задачи (1) существует.
Теорема 17 (Теорема двойственности)
Пусть вектор Куна-Таккера задачи (1) существует. Если значение прямой задачи (1) конечно ( ) в частности, если она имеет решение, то множество решений двойственной задачи (18) непусто и совпадает с множеством векторов Куна-Таккера задачи (1). При этом справедливо соотношение двойственности
) в частности, если она имеет решение, то множество решений двойственной задачи (18) непусто и совпадает с множеством векторов Куна-Таккера задачи (1). При этом справедливо соотношение двойственности
 . (19)
. (19)
98. Показать, что если вектор Куна – Таккера задачи (1) существует, а допустимое множество  двойственной задачи непусто, то она имеет решение. Если же
двойственной задачи непусто, то она имеет решение. Если же  , то
, то  .
.
99. Для задачи

построить двойственную и найти её решение. Убедится в справедливости соотношения (19).
Теорема 18 (Теорема Куна-Таккера в форме двойственности).
Пусть вектор Куна-Таккера задачи (1) существует. Тогда точка  является решением задачи (1) в том и только том случае, если существует вектор
является решением задачи (1) в том и только том случае, если существует вектор  такой, что справедливо соотношение двойственности
такой, что справедливо соотношение двойственности
 , (20)
, (20)
равносильное условиям
 ,
,
 .
.
Множество векторов  , удовлетворяющее (20), совпадает с множеством решений двойственной задачи (18) или же с множеством векторов Куна-Таккера прямой задачи (1).
, удовлетворяющее (20), совпадает с множеством решений двойственной задачи (18) или же с множеством векторов Куна-Таккера прямой задачи (1).
100. Решить задачу:

 - заданные числа.
- заданные числа.
Литература
1. Давыдов Н.А., Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу. –М.: Просвещение, 1964.
2. Лидский В.Б., Овсянников Л.В., Тулайков А.Н., Шабунин М.И. Задачи по элементарной математике. –М.: Наука, 1965.
3. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. –М.: Наука, 1984.
4. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации.
|
|
|
–М.: Наука, 1986.
5. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. –М.: Высшая школа, 1986.

 2020-01-14
2020-01-14 155
155







