Непустое множество  называется выпуклым, если
называется выпуклым, если  при всех
при всех  ,
,  .
.
Функция 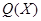 , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется выпуклой, если
, называется выпуклой, если
 (11)
(11)
при всех  ,
, 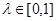 . Если при всех
. Если при всех  ,
, 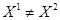 ,
, 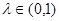 неравенство (11) выполняется как строгое, то
неравенство (11) выполняется как строгое, то 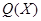 называется строго выпуклой.
называется строго выпуклой.
Функция 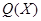 , определенная на выпуклом множестве
, определенная на выпуклом множестве 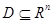 , называется сильно выпуклой с константой
, называется сильно выпуклой с константой  , если
, если

при всех  ,
, 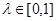 .
.
Ниже приведены необходимые и достаточные условия выпуклости и сильной выпуклости дифференцируемых функций. Для краткости формулировок выпуклые функции рассматриваются как сильно выпуклые с параметром  .
.
Теорема 9 (Первый дифференциальный критерий сильной выпуклости)
Пусть функция 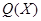 дифференцируема на выпуклом множестве
дифференцируема на выпуклом множестве 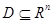 . Тогда для того, чтобы
. Тогда для того, чтобы 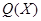 была сильно выпуклой с параметром
была сильно выпуклой с параметром 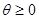 на
на  , необходимо и достаточно выполнения условия:
, необходимо и достаточно выполнения условия:
 , при всех
, при всех  .
.
Теорема 10 (Второй дифференциальный критерий сильной выпуклости)
Пусть функция 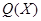 непрерывно дифференцируема на выпуклом множестве
непрерывно дифференцируема на выпуклом множестве 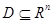 . Тогда для того, чтобы
. Тогда для того, чтобы 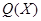 была сильно выпуклой с параметром
была сильно выпуклой с параметром 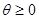 на
на  , необходимо и достаточно выполнения условия:
, необходимо и достаточно выполнения условия:
 , при всех
, при всех  .
.
Теорема 11 (Третий дифференциальный критерий сильной выпуклости)
Пусть 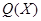 дважды непрерывно дифференцируема на выпуклом множестве
дважды непрерывно дифференцируема на выпуклом множестве 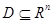 , причем внутренность множества
, причем внутренность множества  не пуста (
не пуста (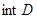
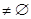 ). Тогда для того, чтобы
). Тогда для того, чтобы  была сильно выпуклой с параметром
была сильно выпуклой с параметром 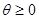 на
на  , необходимо и достаточно выполнения условия:
, необходимо и достаточно выполнения условия:
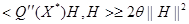 для всех
для всех  .
.
37. Показать, что множество  выпукло тогда и только тогда, когда
выпукло тогда и только тогда, когда  при всех
при всех  . Здесь
. Здесь  - алгебраическая сумма множеств
- алгебраическая сумма множеств  (
( ).
).
38. Являются ли выпуклыми множествами следующие множества на плоскости:
а) круг 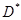 с центром в начале координат;
с центром в начале координат;
в) часть круга  , получающаяся из него путём вырезания сектора, лежащего в правом квадранте.
, получающаяся из него путём вырезания сектора, лежащего в правом квадранте.
39. Верно ли, что объединение и пересечение двух выпуклых множеств выпукло?
40. Пусть 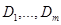 - выпуклые множества,
- выпуклые множества,  - произвольные числа. Доказать, что множество
- произвольные числа. Доказать, что множество  выпукло.
выпукло.
41. Перечислить все выпуклые множества, принадлежащие числовой прямой  .
.
42. Показать, что следующие множества являются выпуклыми:
а) 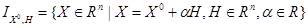 - прямая, проходящая через точку
- прямая, проходящая через точку  в направлении
в направлении  ;
;
в)  - луч, выходящий из точки
- луч, выходящий из точки  в направлении
в направлении  ;
;
с)  - гиперплоскость с нормалью
- гиперплоскость с нормалью  (
( )
) 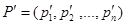 ;
;
d)  ,
,
 - порождаемые гиперплоскостью с нормалью
- порождаемые гиперплоскостью с нормалью  (
( ) полупространства. Здесь
) полупространства. Здесь  .
.
43. Показать, что множество 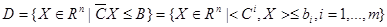 , где
, где  - некоторая матрица размера (
- некоторая матрица размера ( ) со строками
) со строками 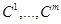 ,
,  , является выпуклым.
, является выпуклым.
44. Показать, что множество  является выпуклым. Здесь
является выпуклым. Здесь  , - заданные числа.
, - заданные числа.
Точка 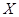 выпуклого множества
выпуклого множества  называется крайней, если её нельзя представить в виде
называется крайней, если её нельзя представить в виде 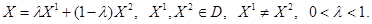
45. Определить все крайние точки множества  , заданного в задаче 44.
, заданного в задаче 44.
46. Определить все крайние точки множества  , где
, где  .
.
47. Указать все крайние точки множества  , определённого в задаче 42.
, определённого в задаче 42.
В задачах 48-53 множество  предполагается выпуклым.
предполагается выпуклым.
48. Доказать, что функция  - выпукла, если
- выпукла, если  выпукла и
выпукла и  .
.
49. Доказать, что функция 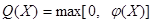 - выпукла, если
- выпукла, если  выпукла,
выпукла,  .
.
50. Проверить, что функция  - выпукла на
- выпукла на 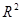 .
.
51. Пусть  - выпуклые функции на множестве
- выпуклые функции на множестве  . Доказать, что функция
. Доказать, что функция  - выпукла на
- выпукла на  .
.
52. Пусть  - выпуклые функции на множестве
- выпуклые функции на множестве  ,
, 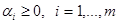 , и хотя бы при одном
, и хотя бы при одном  функция
функция 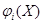 строго (сильно) выпукла,
строго (сильно) выпукла,  . Доказать, что
. Доказать, что  - строго (сильно) выпукла на
- строго (сильно) выпукла на  .
.
53. Доказать, что функция 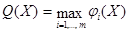 - выпукла на
- выпукла на  , если функции
, если функции 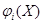 ,
,  , выпуклы на
, выпуклы на  .
.
54. Пусть  - выпуклая функция на выпуклом множестве
- выпуклая функция на выпуклом множестве  . Показать, что
. Показать, что  при всех
при всех  , для которых
, для которых  .
.
55. Доказать, что функция  сильно выпукла на
сильно выпукла на  ,
, 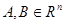 .
.
56. Доказать, что строго вогнутая функция может достигать своего минимального значения только в крайних точках выпуклого множества  , на котором она определена.
, на котором она определена.
57. Найти максимальное значение функции  при выполнении ограничений:
при выполнении ограничений:
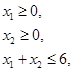

58. Пусть функция  - непрерывная, монотонно неубывающая функция на отрезке
- непрерывная, монотонно неубывающая функция на отрезке  . Показать, что функция
. Показать, что функция  является выпуклой на отрезке
является выпуклой на отрезке  .
.
59. Проверить, что функция  выпукла на
выпукла на  .
.
Задача
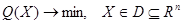 (12)
(12)
называется выпуклой, если  - выпуклое множество, а
- выпуклое множество, а  выпуклая функция на
выпуклая функция на  .
.
60. Доказать, что в выпуклой задаче любое её локальное решение является также и глобальным.
61. Пусть функция  выпукла на
выпукла на  и дифференцируема в точке
и дифференцируема в точке 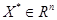 . Доказать, что если
. Доказать, что если  , то
, то  - точка минимума функции
- точка минимума функции  на
на  .
.
62. Известно, что выпуклая задача (12) имеет решение. Доказать, что тогда множество её решений выпукло, если при этом  строго выпукла на
строго выпукла на  , то решение задачи (12) единственно.
, то решение задачи (12) единственно.
 2020-01-14
2020-01-14 402
402








