Формализация задачи (или словесно-формульное описание)

 

Формализация задачи или словесно-формульное описание задачи - определяются расчетные формулы и условия, связывающие входные, промежуточные и выходные величины, этот раздел служит для определения последовательности и способов преобразования исходный величин в результатные.

Исходная функция 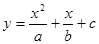 (1)

Первая производная      (2)

Вторая производная

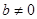Критическая точка , где .Если 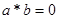, то решить задачу невозможно.

Если 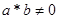, то находим:

- экстремум функции: если y^”(x₁)>0, то х₁ – точка минимума, если y^”(x₁)<0, то х₁ – точка максимума,

- у(а₁), у(х₁) и у(а₂), среди которых определяет наибольшее и наименьшее значение функции.

На заданном интервале [ a₁; a₂ ] рассчитаем шаг табулирования функции .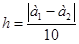

Для табулирования функции первой значение х=а₁

Следующее значение х=x+h

Последнее значение x<=a₂,

Значение y рассчитывается по формуле (1), y’  - по формуле (2)

Алгоритм задачи

 

Для решения данной задачи использовались внутренние процедуры и функции, поэтому в этом разделе представлены алгоритмы основной (главной программы) и алгоритмы каждой из подпрограмм – таблица № 4.

 

Таблица №4 – Описание подпрограмм

 

Идентификатор подпрограммы	Тип подпрограммы	Возвращаемые величины	Назначение
Y	Функция	y	Вычисляет значение функции
dy	Функция	dy	Вычисляет первую производную
Min_max2	Процедура	-	Определяет минимум и максимум из двух величин F1 и F2
Min_max3	Процедура	-	Определяет минимум и максимум из трех величин F1, F2, F3

 

Алгоритм основной программы представлен на рис. 1.

 

Рисунок 1 – Логическая схема основной программы

 

 

Алгоритм функции y представлен на рис. 2

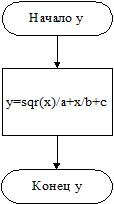
Рисунок 2 – Логическая схема подпрограммы – функции у

Алгоритм функции dy представлен на рис. 3.

 

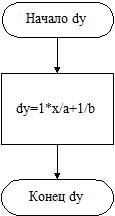
Рисунок 3 – Логическая схема подпрограммы - функции dy

Алгоритм подпрограммы min_max_2 представлен на рис. 4.

Рисунок 4 – Логическая схема подпрограммы-процедуры min_max_2

 

Алгоритм подпрограммы min_max_3 представлен на рис. 5.

 

 

Рисунок 5 – Логическая схема подпрограммы-процедуры min_max3