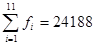Розв’язання. Медіана ділить усі оцінки навпіл. Двадцять перший член дорівнює 3, двадцять другий член дорівнює 3. Медіана дорівнює 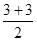 = 3. Бачимо, що із 42 оцінок 21 не перевищує 6, отже, половина оцінок складається з 3 і 6, що свідчить про незадовільну якість знань.
= 3. Бачимо, що із 42 оцінок 21 не перевищує 6, отже, половина оцінок складається з 3 і 6, що свідчить про незадовільну якість знань.
Середні значення
Статистика оперує такими середніми значеннями: середне арифметичне, середнє квадратичне, середнє геометричне.
Середнє арифметичне. Нехай ми маємо n об’єктів, у яких виміряна деяка характеристика, що має значення х 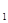 , х
, х 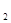 ,…, х
,…, х 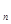 .
.
Середнім значенням (або середнім арифметичним) називається таке число 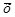 , яке дістають діленням суми всіх даних вибірки х
, яке дістають діленням суми всіх даних вибірки х 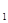 , х
, х 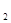 , х
, х 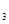 , …, х
, …, х  на число цих даних n.
на число цих даних n.
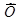 =
= 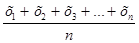 ,
,
або 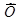 =
= 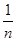
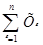 (Σ – знак суми – «сигма» велика).
(Σ – знак суми – «сигма» велика).
Приклади. 1) Протягом перших п’яти днів березня температура повітря, вимірювана о 8 год. ранку, становила 3 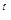 , 5
, 5 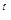 , 4
, 4 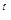 , 1
, 1 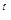 , 2
, 2 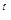 . Знайти середню температуру за ці дні.
. Знайти середню температуру за ці дні.
Маємо: 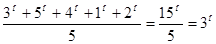 .
.
2) З двох учнів треба вибрати одного в баскетбольну команду. Відомі кількості їхніх влучень м’яча в корзину на кожні десять кидків під час тренувань.
| Номер тренування | 1 | 2 | 3 | 4 | 5 |
| Кількість влучень | Перший учень | ||||
| 4 | 3 | 5 | 3 | 6 | |
| Другий учень | |||||
| 5 | 4 | 3 | 6 | 5 | |
Розв’язання. Знаходимо середню кількість влучень.
Для першого учня:
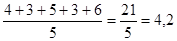 .
.
Для другого учня:
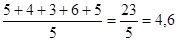 .
.
Отже, в команду слід узяти другого учня.
Розглянемо деякі властивості середнього арифметичного.
1) Знайдемо відхилення l кожного значення х 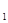 від середнього
від середнього 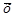 . Різниця (х -
. Різниця (х - 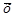 ) може бути від’ємною або додатною. Сума всіх n відхилень дорівнює нулю. Проілюструємо цю властивість на прикладі.
) може бути від’ємною або додатною. Сума всіх n відхилень дорівнює нулю. Проілюструємо цю властивість на прикладі.
Вихідні дані: (0; 0; 1; 1; 3; 3; 3; 5); n= 8; 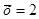 .
.
| Значення | Середнє арифметичне | Відхилення |
| 0 0 1 1 3 3 3 5 | 2 2 2 2 2 2 2 2 | -2 -2 -1 -1 1 1 1 3 - 0 |
2) Якщо до кожного результату спостережень додати деяке число с (константу), то середнє арифметичне 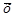 перетвориться на (
перетвориться на (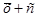 ). Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6; 6; 8; 8; 8; 10, середнє арифметичне яких (5+5+6+6+8+8+8+10): 8 = 7. Середнє на 5 одиниць більше.
). Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6; 6; 8; 8; 8; 10, середнє арифметичне яких (5+5+6+6+8+8+8+10): 8 = 7. Середнє на 5 одиниць більше.
3) Якщо кожне значення сукупності із середнім 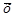 помножити на константу с, то середнє арифметичне стане с
помножити на константу с, то середнє арифметичне стане с 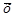 . Перевірте властивість, використовуючи попередні дані.
. Перевірте властивість, використовуючи попередні дані.
Якщо величини деяких даних повторюються, то середнє арифметичне визначається за формулою
 ,
,
де f 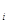 - частота повторення результату х
- частота повторення результату х 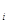 .
.
Приклади. 1) Протягом двадцяти днів серпня температура повітря вранці була такою: 17є; 18є; 19є; 20є; 18є; 18є; 18є; 19є; 19є; 20є; 20є; 19є; 19є; 19є; 20є; 19є; 18є; 17є; 16є; 19є.
Знайти середню температуру за цими даними.
Тут окремі значення (17є; 18є; 19є; 20є) повторюються. Середня температура дорівнює:
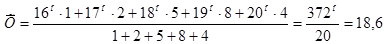 .
.
Подаємо запис обчислення середнього арифметичного при повторенні деяких даних у вигляді таблиці:
| Вихідні дані | х 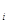
| Частота f 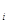
| x  f f 
| Остаточне обчислення |
| 2 6 10 2 6 10 3 6 11 4 6 12 4 8 12 4 9 15 5 9 15 5 9 15
| 2 3 4 5 6 8 9 10 11 12 15 | 2 1 3 2 4 1 3 2 1 2 3 | 4 3 12 10 24 8 27 20 11 24 45 |
де і = 1, 2, 3,…, 11 |
| n=
| ||||
2) За контрольну роботу учні одержали такі оцінки:
| Оцінка, бали | 12 | 9 | 6 | 3 |
| Кількість учнів | 6 | 7 | 4 | 17 |
Чи достатньо засвоєний матеріал?
Знайдемо середнє значення оцінок.
 .
.
Ця оцінка є задовільною. Але частота оцінки «2» (мода) дуже висока, вона дорівнює 17. Отже, матеріал засвоєний учнями недостатньо.
Середнє квадратичне відхилення. Ми вже встановили, що сума відхилень даних від середнього значення дорівнює нулю. Тому якби ми вирішили шукати середній показник відхилень, то він також дорівнював би нулю. В статистиці користуються іншим показником – середнім квадратичним відхиленням, який знаходять так: усі відхилення підносять до квадрата; знаходять середнє арифметичне цих квадратів; із знайденого середнього арифметичного добувають квадратний корінь. Середнє квадратичне відхилення позначають грецькою буквою δ («сигма» мала):
Значення х 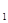
| Середнє арифметичне
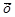
| Відхилення
(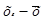 ) )
| Квадрат
відхилення
(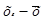 )І )І
| Квадратичне відхилення δ |
| 5 8 10 12 17 20 | -7 -4 -2 0 5 8 | 49 16 4 0 25 64 | ||
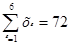
|
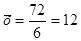
|
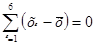
|
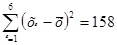
| Δ=
=   =
= =
= 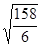 = = 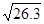 ≈
≈ 5,13 ≈
≈ 5,13
|
δ = 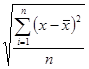 .
.
Знаходження середнього квадратичного відхилення подано в таблиці.
У статистиці користуються також величиною δ² (квадрат середнього квадратичного відхилення), яку називають дисперсією.
Середнє геометричне n доданих чисел х 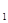 , х
, х 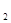 , х
, х 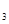 , …, х
, …, х 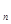 визначається виразом m
визначається виразом m 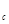 =
= 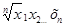 , тобто середнє геометричне
, тобто середнє геометричне 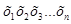 є корінь n-го добутку всіх
є корінь n-го добутку всіх 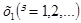 .
.
У випадку двох чисел а і b середнє геометричне називають середнім пропорційним цих чисел. З рівності m 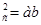 випливає, що а:m
випливає, що а:m 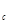 = m
= m 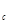 :b.
:b.
На практиці окремим особам, організаціям, керівникам підприємств доводиться розв’язувати різноманітні задачі, пов’язані з використанням понять моди, медіани, середнього. Наприклад, яких розмірів дитячого взуття треба випускати більше,ніж інших; на якому з міських маршрутів має бути автобусів більше, ніж на решті; якого розміру спортивних костюмів треба виготовити найбільше для учнів 10-11 класів тощо.
 2020-01-14
2020-01-14 121
121

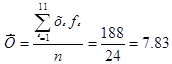 ,
,