Обслуживание требований без задержек

 

Установим NP трудность в сильном смысле 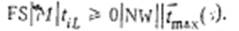В этой задаче условие означает что требование I не обслуживается прибором L При такой интерпретации нулевых длительностей оптимальное расписание без задержек необязательно принадлежит классу перестановленных расписаний.

Другими — словами, задач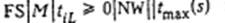и  и 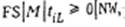 в данном случае не эквивалентны. Напомним, что задач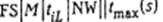и  и 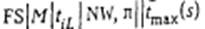эквивалентны, если все  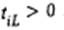либо среди f._t имеются равные нулю и запись  означает, что длительность. Справедлива

Теорема 1.1. Задача 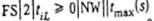 является NP трудной в сильном смысле, если условие 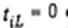означает, что требование i прибором L не обслуживается.

Доказательство. Сформулируем соответствующую задачу распознавания: определить, существует ли расписание s°, при котором 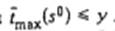 для заданного числа у. Покажем, что к этой задаче сводится задача о 3-разбиении. Для преобразования входной информации задачи о 3-раэбиении во входную информацию индивидуальной задачи распознавания необходимо значения 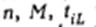и у выразить через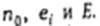

Положим 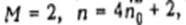и разобьем множество N на две группы: и-требования, обозначаемые U_ij  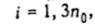и v-требовання, обозначаемые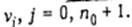

Положим 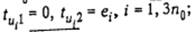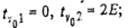, и зададим / 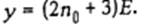. Покажем, что в построенной задаче расписание S°, при котором 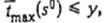существует тогда и только тогда, когда имеет решение задача о 3-разбиеиии. имеет решение задача о 3 разбиений.

1. Пусть задача о 3-разбиении имеет решение и 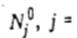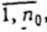найденные трехэлементные подмножества элементов множества N ⁰. Через  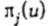 обозначим произвольную перестановку u-требований с номерами из множества 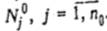. Прибор 1 функционирует без простоев во временном интервале 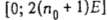], а прибор 2 - в интервале [0; у]. При этом прибор 1 в интервале  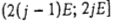 обслуживает требование  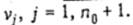. Прибор 2 в интервале  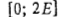обслуживает требование v₀, а в каждом из интервалов 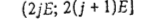- последовательность требований  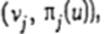Требование  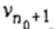обслуживается прибором 2 в интервале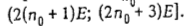

2. Пусть существует расписание s°. Так как 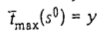и прибор 2 функционирует в интервале [0; у] без простоев.

 

Рис.(1.1)

 

Прибор 1 завершает обслуживание всех требований не раньше момента времени у - Е. С учетом того, что задержки запрещены, последним требованием, которое обслуживает прибор 2, будет некоторое v-требование, а прибор 1 должен функционировать без простоев в интервале 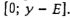. Поскольку требования 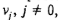, не отличаются друг от друга по длительностям обслуживания, не нарушая общности можно считать, что они обслуживаются прибором I в порядке возрастания их номеров. Отсюда сразу следует, что требования 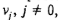, обслуживаются при расписании s° так же, как и при расписании, представленном на рис. 1.1. Требование v_c обслуживается прибором 2 в интервале 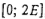, так как это единственный незанятый подинтервал длины 2Е интервала 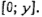Требования щ должны обслуживаться прибором 2 в интервалах 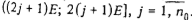. Обозначая через 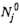множество номеров и-требований, обслуживаемых прибором 2 в интервале 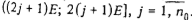, получаем решение задача о 3-разбиении. Тем самым за 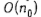действий задача о 3-раз-биении сведена к задаче о существовании расписания S°. Теорема доказана.

Теорема 2. Задача 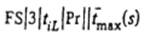является NP-трудной в сильном смысле.

Теорема 3. Задача 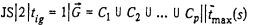является NP-трудной в сильном смысле.

Доказательство. Сформулируем соответствующую задачу распознавания. В обслуживающую систему, состоящую из двух приборов А и В, в момент времени d=0 поступает частично упорядоченное множество требований

N{1,2...., л}.. Каждая компонента связности графа редукции отношения -, заданного на N, является цепью. Длительность выполнения каждой операции равна единице. Требуется определить, существует ли расписание S°, при котором 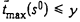 для заданного значения у.

Построим псевдополнномиальное сведение задачи о 3-разбиении к сформулированной задаче распознавания.

Положим: 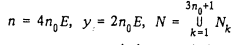 , где

 

 

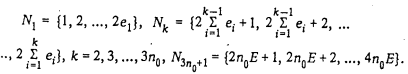
На множестве N заладим отношение -, полагай / - I тогда и только тогда, когда 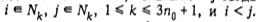. Очевидно, каждая компонента связности графа редукции этого отношения представляет собой цепь.

Пусть процесс обслуживания каждого требования 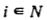состоит в выполнении единственной операции. Для требований из множества N₁ положим L¹ = (В) при 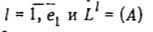. Для каждого 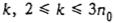, положим

 

 

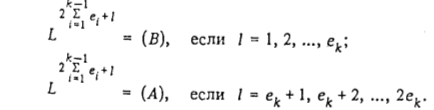
Для требования из множества 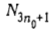 - линейно –упорядоченное и число его элементов равно 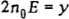, то при любом расписаний с общим временем обслуживания требований, равным у, требования множества N_{3n +1} должны обслуживаться непрерывно одно за другим начиная с момента времени d = 0. На рис. 2 представлен фрагмент расписания обслуживания требований множества  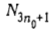при котором общее время обслуживания требований равно у. Это расписание является периодическим с периодом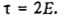

 

Рис(1.2)

 

Таким образом, обслуживание требований множества 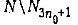при любом расписании с общим временем обслуживания требований, равным у, может быть осуществлено только в тех единичных интервалах, которые определяются последовательностью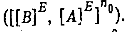

Покажем, что расписание S⁰ можно построить тогда и только тогда, когда имеет решение задача о 3-раэбиении. Пусть существует разбиение множества № на n₀ трехэлементных подмножеств 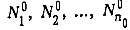таких, что 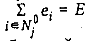при j=1,0. Тогда, обслуживая множество требований  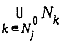 интервале 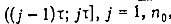, в соответствии с отношением получаем расписание с общим временем обслуживания требований, равным у.

Пусть существует расписание S°, при котором 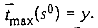.Так как суммарная длительность обслуживания всех требований прибором А (прибором В) равна у, то при расписании S как прибор А, так и прибор В в интервале [0; у] не простаивает. По условию обслуживание каждого требования 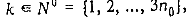для которого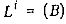

Учитывая, что в построенном при доказательстве теоремы 3 примере процесс обслуживания каждого требования состоит из единственной операции, можно сделать вывод о том, что и задача 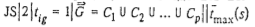является NP-трудной в сильном смысле.

 

Алгоритм

Этап 1. Построить бесконтурный граф 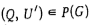 в результате выполнения следующего шага не более чем q - 1 раз. Первоначально положить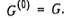

Пусть после выполнения 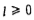шагов получен смешанный граф 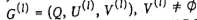, у которого l вершин отмечено и существует неотмеченная вершина i, в которую не заходит ни одна дуга, исходящая из неотмеченной вершины. (Если такой вершины нет, то в графе (Q,U) содержится контур. Конец.)

Шаг 1 + 1. Отметить вершину i и в случае, если в графе G⁽¹⁾ есть ребра, инцидентные этой вершине, то заменить их исходящими из нее дугами. Полученный в результате граф обозначить G^(J+1) = (Q,U^(l+1), V^(l+1)). Если V^(l+1) = 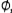, то бесконтурный граф построен: 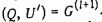. В противном случае выполнить этот шаг, заменив l на l + 1.

Этап 2. В соответствии с алгоритмом 3.1 построить которое допустимо относительно ориентированного графа 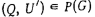и смешанного графа G. Конец.

Нетрудно убедиться в корректности описанного алгоритма, что и завершает доказательство теоремы.

Очевидно, трудоемкость этапа 1 алгоритма не превосходит 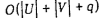 и, следовательно, общая трудоемкость построения активного расписания, допустимого относительно смешанного графа G, не превосходит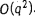

Если для каждого графа G⁽¹⁾ в алгоритме рассматривать все возможные варианты выбора вершины i, то получим все множество P(G) = {G₁ G₂,..., G} бесконтурных графов, порождаемых смешанным графом G. Следовательно, все множество допустимых относительно G активных расписаний можно построить за 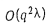элементарных действий.

Пример 1. В условиях примера 3.1 (см. рис. 1) воспользуемся алгоритмом 2 для построения допустимого относительно С = (Q, V, V) расписания.

На этапе 1 алгоритма строим бесконтурный ориентированный граф из множества P{G). Положим G⁰= G и выберем на шаг 1 вершину 1, в которую не заходит ни одна дуга. Отметим вершину 1 и заменим дугами инцидентные ей ребра. Получим смешанный граф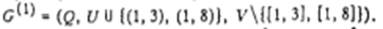

На шаге 2 аналогичные преобразования проделаем для вершины 3, на шаге 3 — для вершины 4, на шаге 4 - для вершины 2, на шаге 5 - для вершины 9. Полученный в результате граф 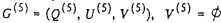 представлен на рис1 в виде сетевого графика.

 

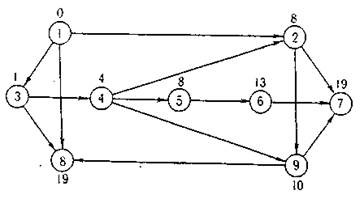
Рис (2.1)

 

На этапе 2 воспользуемся алгоритмом 1 для построения активного расписания, допустимого относительно ориентированного графа 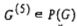. Сначала сформируем списки потомков и списки предшественников каждой вершины 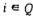, затем распределим вершины графа  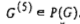по рангам  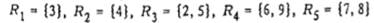наконец, по формуле 1 вычислим значения 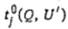для всех вершин  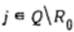последовательно в порядке неубывания рангов вершин. Полученные значения 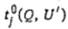указаны около соответствующих вершин  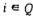сетевого графика.

 

Последовательный анализ вариантов

Выше рассматривались вопросы построения активного расписания, допустимого относительно ориентированного или смешанного графа. Было Сказано, что не более чем за 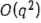элементарных действий можно построить допустимое расписание либо установить невозможность построения такого расписания.

Если на каждом шаге алгоритма 2 рассматривать все возможные варианты выбора вершины i, в которую не заходит ни одна исходящая из: неотмеченной вершины дуги, то можно получить все множество P(G={G₁,G₂….G} бесконтурных графов порождаемых графом G = (Q, U, V). Задачу можно решить в результате построения активных расписаний, допустимых относительно графов 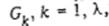, и выбора среди них расписания S* минимизирующего значение F(s)- Трудоемкость полного перебора всех активных расписаний задачи  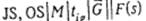может быть ограничена величиной 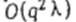при условии, что для вычисления функции F(s) требуется не более  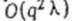 элементарных действий.

К сожалению, мощность множества P(G) растет в обшей случае экспоненциально с ростом параметров задачи n и М. Например, для задачи 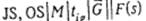 значение  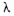 равно n!. Граф 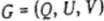при этом является полным не ориентированным: 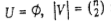и q=n. Рост значений |v| и  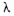показан в табл. 1

 

Таблица 1.

 

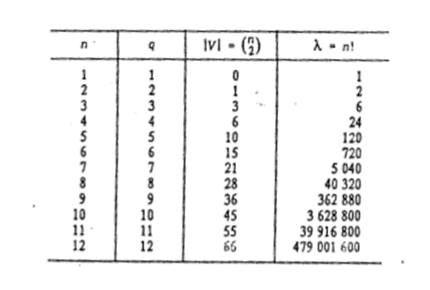
Сокращение числа перебираемых расписании можно обеспечить методом последовательного анализа вариантов. Для организации целенаправленного перебора графов множества P(G)будем использовать процедуру последовательного разбиения множества P(G) на подмножества.

При этом подмножество P(G) сначала разбивается va подмножества P(G¹), P(G²)…… P(G^k), где G^k, k=1, h- графы, получаемые из 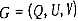 в результате замены одного или нескольких ребер V дугами. Затем одно из множеств P(G^k), например P(G^l), в свою очередь разбивается на подмножества P(G^h+1), P(G^h+2),..., P(G^h+p), результате получаем разбиение исходного множества

Этот процесс удобно представлять „растущим" выходящим деревом 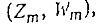где Z_m - множество его вершина.

Множество всех конечных вершин дерева (Zm, Wm) будем обозначать через Zm. При выполнении условия а) получаем точное значение f(C'). Нетрудно видеть, что из условия б) следует соотношение 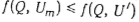 для любого графа 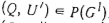. При выполнении условия в) существует граф  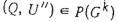такой, что 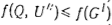. Следовательно, при поиске оптимального расписания граф G¹ можно исключить из рассмотрения, если условие б) или в) выполняется.