Обзор существующих методов вейвлет-преобразования и типовых вейвлетов для определения их применяемости в системах обнаружения вторжений

 

 

Вейвлеты стали необходимым математическим инструментом при анализе и обработке сигналов нестационарных во времени или неоднородных в пространств. В рамках проводимой выпускной работы необходимо определить возможность использования вейвлетов в качестве образов сетевых атак в системах обнаружения вторжений. Для этого проведем обзор проведенных на данный момент исследований и составим классификацию методов вейвлет-преобразования и используемых в них вейвлетов с целью оценки их применения в условиях распознавания сетевой атаки. При практическом использовании вейвлетов необходимо уделять достаточное внимание проверке их работоспособности и эффективности для поставленных целей по сравнению с известными методами обработки и анализа.

Вейвлет-преобразование представляет собой свертку вейвлет-функции с сигналом. Вейвлет-преобразование переводит сигнал из временного представления в частотно-временное. Общий принцип построения базиса вейвлет-преобразования состоит в использовании масштабного преобразования и смещений, и любой применяемый вейвлет порождает целую систему функций.

Выбор анализирующего вейвлета не определен заранее, а выбирается в соответствии с решаемой проблемой. Неудачный выбор конкретной формы вейвлета может привести к невозможности выполнения поставленной задачи. Особенностью вейвлет-анализа является то, что в нем можно использовать большое число основных вейвлет-функций, реализующих различные варианты соотношения между частотой и локализацией при анализе сигнала. Поэтому при исследовании имеется возможность выбора между семействами вейвлетных функций и гибкого применения тех, которые наиболее эффективно решают конкретную задачу.

Вейвлет-преобразование схоже с оконным преобразованием Фурье, но имеет иную оценочную функцию. Основное различие заключается в следующем: преобразование Фурье раскладывает сигнал на составляющие в виде синусов и косинусов, т.е. функций, локализованных в Фурье-пространстве; напротив, вейвлет-преобразование использует функции, локализованные как в реальном, так и в в Фурье-пространстве.

Вейвлет можно представить себе как некоторую функцию, осциллирующую в ограниченном интервале подобно волне и затухающего вне него.

После рассмотрения существующих методов формирования вейвлетов, описанные в различных исследовательских работах, посвященных вейвлет-анализу, можно составить общую классификацию методов вейвлет-преобразований, отображенную на рисунке 1.

 

 

Рисунок 1 – Классификация методов вейвлет-преобразований

 

Дискретное вейвлет-преобразование (ДВП). Данный метод возвращает вектор данных той же длины, что и входной. Обычно, даже в этом векторе многие данные почти равны нулю. Это соответствует факту, что он раскладывается на набор вейвлетов (функций), которые ортогональны к их параллельному переносу и масштабированию. Следовательно, мы раскладываем подобный сигнал на то же самое или меньшее число коэффициентов вейвлет-спектра, что и количество точек данных сигнала. Подобный вейвлет-спектр весьма хорош для обработки и сжатия сигналов, например, поскольку мы не получаем здесь избыточной информации.

Дискретное вейвлет-преобразование запишется следующим образом:

 

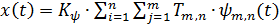                     ,            (1)                    

где  – вейвлет коэффициенты;

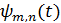   – анализирующая вейвлет-функция;

    – постоянная нормировки.

Первое ДВП было придумано венгерским математиком Альфредом Хааром. Для входного сигнала, представленного массивом 2ⁿ чисел, вейвлет-преобразование Хаара просто группирует элементы по 2 и образует от них суммы и разности. Группировка сумм проводится рекурсивно для образования следующего уровня разложения. В итоге получается 2ⁿ−1 разность и 1 общая сумма.

Базисная функция Хаара определяется соотношением:

    (2)

Любые функции, полученные с помощью этого базисного вейвлета путем масштабных преобразований и переносов, имеют единичную форму и ортогональны.

Также распространенный набор дискретных вейвлет-преобразований был сформулирован бельгийским математиком Ингрид Добеши. Он основан на использовании рекуррентных соотношений для вычисления всё более точных выборок неявно заданной функции материнского вейвлета с удвоением разрешения при переходе к следующему уровню (масштабу). В своей основополагающей работе Добеши выводит семейство вейвлетов, первый из которых является вейвлетом Хаара.

Подробнее о дискретном вейвлет-преобразовании и конструировании вейвлетов Харра и Добеши можно узнать из работ Дьяконова В.П. [5],  Демина И.М. [4] и Добеши И [3].

Непрерывное вейвлет-преобразование. Данный метод, напротив, возвращает массив на одно измерение больше входных данных. Для одномерных данных мы получаем изображение плоскости время-частота. Можно легко проследить изменение частот сигнала в течение длительности сигнала и сравнивать этот спектр со спектрами других сигналов. Поскольку здесь используется неортогональный набор вейвлетов, данные высоко коррелированы и обладают большой избыточностью. Это помогает видеть результат в более близком человеческому восприятию виде.

Для непрерывного вейвлет-преобразования используется следующая формула:

(3)

где x(t) – функция исходного сигнала;

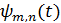   – анализирующая вейвлет-функция.

Подробнее непрерывное вейвлет-преобразование описывается в трудах Дьяконова В.П. [5] и Астафьевой Н.М [1].

Вейвлетные разложения с использованием сплайнов. Сплайн – это функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим многочленом (полиномом). Сплайн-вейвлеты имеют ограниченное число непрерывных производных из-за их связи с некоторыми линейными комбинациями оцифрованного набора.

Применение сплайн-вейвлетов описано в работах Смоленцева Н.К [9] и Демьяновича Ю.К. [2].

Использование биортогональных вейвлетов. Для обеспечения полной симметрии и точной реконструкции одновременно применяют биортогональные вейвлеты, которые строятся с использованием двух ортогональных друг другу вейвлет-базисов. В отличии от вейвлетов Добеши, биортогональные вейвлеты обладают большей свободной выбора нулевых моментов, что приводит к лучшим результатам при сжатии информации.

Подробно конструирование биортогональных вейвлет-базисов описывается в работе Исаева Ю.Н. [6].

Наличие соотношений на двух масштабах является характерной чертой построения вейвлет-пакетов. Основная идея их создания заключается в последовательном расщеплении полосы частот. Это семейство вейвлетов образует базис вейвлет-пакетов с фиксированным масштабом.

Анализ адаптивных алгоритмов вейвлет-пакетов представлен в работе Можарова Г.П. [8].

Построение фреймов – неортогональных вейвлетов, обладающих некоторыми границами. Важный особый класс фреймов представлен базисами Рисса.

Подробнее фреймы и системы Рисса описаны в работе Даффина и Шеффера, Бари Н.К, а также в статье Томашевского С.В. [10].  

Построение вейвлетов с использованием сглаживающей функции b(x), чтобы наложить дополнительные условия, которые будут необходимы и достаточны для того, чтобы результат оказался непрерывным в пространстве.

Использование сглаживающей функции описано в работе Дремина И.М., Иванова О.В и Нечитайло В.А. [4].

Построение вейвлетов с целыми или дробными масштабными множителями. Использование таких множителей приводит к лучше локализации по частоте. Например, для вейвлетов с масштабным множителем 2 образ сосредоточен в основном в пределах одной октавы (например, p и 2p), тогда как вейвлет-базисы с дробными множителями могут иметь ширину полосы пропускание более узкую, чем данная октава.

Использование масштабных множителей также описано в работе Добеши И. [3].

Таким образом, можно отметить, что математический аппарат вейвлет-преобразований и его практическая польза привлекают к себе внимание исследователей. Уникальные математические свойства вейвлетов сделали их мощным инструментом анализа и последующего синтеза любого сигнала на разных масштабах и в разных точках. Вейвлет-преобразование легко обобщается на множества любых размерностей, отчего могут применяться для построения образов. Однако не существует универсального алгоритма для исключительных разнообразных наборов ситуаций, с которыми приходится сталкиваться при анализе различных сигналов. Необходим выбор метода построения вейвлетов, адекватных поставленной задаче, а также выбор масштабов и характеристик исследуемых сигналов.

Так как в данном исследовании рассматриваемым сигналом является атака в сетевом трафике, который наиболее удобно представлять в виде выборки конкретных значений в различные моменты времени, то самым оптимальным к использованию является дискретное вейвлет-преобразование. Использование остальных методов затруднено из-за их вычислительной сложности, обусловленной привлечением дополнительных функций, и недостаточной изученности.

В рамках дискретного вейвлет-преобразования рассмотрим различные типы вейвлетов и оценим возможность их использования в качестве базис-вейвлетов сетевой атаки.

Классификация основных типов базис-вейвлетов, или материнских вейвлетов, представлена в таблице 1.

 

Наименование вейвлета	Описание	Графическое представление
Вейвлет Хаара	Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими.
Вейвлеты Добеши	Семейство ортогональных вейвлетов с компактным носителем, вычисляемым итерационным путём.
Wave-вейвлет («волна»)	Вейвлет, сконструированный на основе производных функций Гаусса первого порядка
MHAT-вейвлет («Мексиканская шляпа»)	Вейвлет, сконструированный на основе производных функций Гаусса второго порядка
FHAT-вейвлет («Французская шляпа»)	Дискретный вейвлет на основе разрывной функции
Вейвлет Морле	Комплексный вейвлет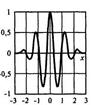

 

Можно отметить, что вейвлеты имеют различную графическую форму, могут быть симметричными, асимметричными и несимметричными, с компактной областью определения и не имеющие таковой, а также иметь различную степень гладкости.

Рассмотрев данный типы базис-вейвлетов можно прийти к выводу, что каждый из них может служить материнским вейвлетом сетевой атаки, полученной при обработке данных сетевого трафика в момент вторжения, и являться образом определенной аномальной активности. Также используя данные вейвлеты как базисы с  использованием  масштабного преобразования и смещений можно создать уникальный вейвлет сетевой атаки, наиболее отражающий ее проявление в сетевом трафике.

Таким образом, использование дискретного вейвлет-преобразования на основе типовых базис-вейвлетов находит свое применение в задаче обнаружения сетевого вторжения.

 

 

Список литературы:

1. Астафьева, Н. М. Вейвлет-анализ: основы теории и примеры применения / М: Успехи физических наук, т. 166, № 11. – 1998 – С. 1145-1170.

2. Демьянович, Ю. К. Введение в теорию вэйвлетов [Текст] – Ю.К. Демьянович, В.А. Ходаковский / Учебное пособие, Санкт-Петербург – 2008 – 50 с.

3. Добеши, И. Десять лекций по вейвлетам [Текст] – И. Добеши, пер. с англ. Е. В. Мищенко; под ред. А. П. Петухова / Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика» – 2004 – 464 с.

4. Дремин, И.М, Вейвлеты и их использование [Текст] – И.М. Дремин, О.В. Иванов, В.А. Нечитайло / М.:Успехи физических наук, т. 171, №5 – 2001 – С. 465-501

5. Дьяконов, В.П. Вейвлеты. От теории к практике [Текст] – В.П. Дьяконов / М.: СОЛОН-Пресс – 2010 – 400с.

6. Исаев Ю.Н. Конструирование биортогональных вейвлет-базисов для оптимального представления сигналов [Текст] – Ю.Н. Исаев / Известия Томского политехнического университета, т. 307, №1 – 2004 – С. 37-42

7. Малла С. Вэйвлеты в обработке сигналов [Текст] – С. Малла, пер. с англ. Я. М. Жилейкина / М.: Мир – 2005 – 671 с.

8. Можаров, Г.П. Сравнительный анализ адаптивных алгоритмов вейвлет-пакетов [Текст] – Г.П. Можаров / Вестник МГТУ им. Н.Э. Баумана. Сер. «Приборостроение», т.106, №1 – 2016 – С. 75-89

9. Смоленцев, Н.К. Основы теории вейвлетов. Вейвлеты в Matlab [Текст] – Н.К. Смоленцев / М.:ДМК Пресс – 2014 – 628 с.

10. Томашевский, С.В. Обобщённые фреймы и системы Рисса [Текст] – С.В. Томашевский / Вестник РУДН. Сер.: Математика, информатика, физика, т№4 – 2014 – С. 5-14