Корневые методы анализа качества

Реферат

Предмет: Теория автоматического управления

Тема: Анализ качества дискретных систем управления

Методы определения качества дискретных систем автоматического управления аналогичны методам определения качества непрерывных систем с учетом некоторых особенностей.

 

1. Оценка качества дискретной системы по переходной функции

 

Порядок использования этого метода рассмотрим на примере.

Пример 1. Рассчитать переходный процесс в заданной дискретной системе (рис. 1), и определить качество переходного процесса при различных значениях T и k_v.

 

 

Рис. 1

 

Решение: Выходной дискретный сигнал равен

 

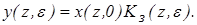
Если x(t) = 1(t), то .

 

Определим передаточную функцию разомкнутой непрерывной части

 

 

Выполним дискретное преобразование

 

 

Передаточная функция замкнутой дискретной системы

 

 

Подставим x(z) и K_з(z,e) в выражение для выходного дискретного сигнала

 

 

При этом

 

.

 

Определим значения полюсов - z_k их число -n и кратность - m.

z₁ = 1, z₂ = 1 - k_vT = A, n = 2, m = 1.

Выражение для переходной функции имеет вид:

 

 

Определим установившееся значение переходной функции:

 

 

Рассчитаем переходную функцию для различных значений параметров системы

1. Пусть k_vT = 1.

 

 

Переходный процесс приведен на рис. 2а. При этом система имеет следующие показатели качества: время регулирования t_p = T; относительное перерегулирование s% = 0; число переколебаний N = 0; период собственных колебаний T₀ = T.

2. Пусть k_vT = 2.

 

 

Переходный процесс приведен на рис. 2б. При этом система находится на границе устойчивости.

3. Пусть k_vT = 1,5.

 

 

Результаты расчета приведены в таблице 1.

 

Таблица 1

n	0	1	2	3	4	5
(-0,5)n	1	-0,5	0,25	-0,125	0,0625	-0,03125
h[nT]	0	1,5	0,75	1,125	0,9375	1,03125

 

Переходный процесс приведен на рис. 2в.

При этом система имеет следующие показатели качества:

 

t_p = (4¸5)T; s% = 50; N = 4; T₀ = 2T.

 

 

Рис. 2

Корневые методы анализа качества

Корневые методы позволяют оценить качество с помощью косвенных показателей качества, при этом анализируется расположение корней характеристического уравнения k_i = ±s_i ±jw_i в комплексной плоскости в пределах основной полосы.

При этом используются следующие косвенные показатели качества:

1. Степень устойчивости .

2. Колебательность m = w₀/s₀.

Демпфирование c = s₀/w₀.