Алгоритм приближенного расчета распада разрыва

    Исходя из изложенных выше соображений, автор считает целесообразным описать один из возможных алгоритмов приближенного расчета распада разрыва, не допускающий убывания энтропии. Конечно, многие его детали уже описывались и в монографиях [5], [9] и в работах других исследователей. Автор считает своим долгом отметить также [10], на которую обратил внимание при подготовке настоящей работы, благодаря ссылке на стр.170 монографии [9]. Для полноты и связности изложения известные уже детали придется повторить. Но некоторые элементы являются новыми и могут представлять практический интерес. Особое внимание уделено аргументации предлагаемых решений.

4.1. Итак, в качестве исходной информации задаются:

- параметры течения в соседних ячейках , ;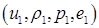

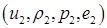- три термодинамических параметра 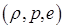 связывает уравнение состояния (1.1) с заданным показателем адиабаты g; вопрос о более сложных уравнениях состояния будет обсуждаться позже (в § 5);

- задается безразмерный параметр 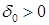, который будет играть роль критерия применимости «звукового приближения».

 

4.2. Расчет начинается с вычисления скоростей звука

(4.1)       ,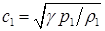  

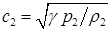
и «пробного» назначения массовых скоростей

(4.2)       ,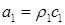   

Заметим, что «волевое» назначение массовых скоростей a₁,a₂ – операция достаточно ответственная и достигает цели только в случае, если обеспечивает достаточно аккуратную аппроксимацию исходных уравнений. Поэтому из возможных различных вариантов, упоминавшихся ранее, выбирается именно этот, поскольку представляет математически обоснованную линеаризацию уравнения для давления Р:

(4.3)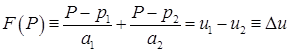                   

Отметим, что это предлагалось, например, в [5] на стр.113.

4.3. В соответствии с изложенным в § 1, вычисляем 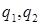 по формулам (1.6).

    Если выполняются два условия:

(4.4)      ,          ,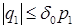

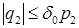полагаем, что достаточным является «звуковой» расчет распада разрыва. В этом случае, в соответствии с (1.7), назначаем:

             

            

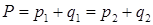
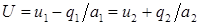
Для оценки изменения энтропии можно воспользоваться приближенной формулой (2.7):

(4.5)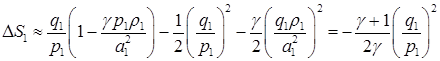    

Очевидно, что совершенно аналогично:

         

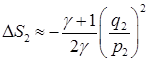
Следовательно, при выполнении условий (4.4) получаем:

(4.6)        ,      .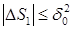

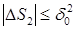    Если «примириться» со столь незначительным (при достаточно малом значении параметра 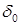) убыванием энтропии, можно вычислять величины r₃,r₄ по формулам (1.8), величины е₃,е₄ – по формулам (1.4), величины D₁,D₂ – по формулам (1.5). Это те формулы, которые предлагались в схеме С, однако со следующим существенным замечанием. Именно благодаря назначению a₁,a₂ по формулам (4.2) достигается обращение в нуль первого слагаемого в формуле (4.5). При назначении a₁,a₂ формулами (2.1) или (2.4), по крайней мере, для одной из величин  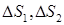этого не будет, и она будет иметь не второй, а лишь первый порядок относительно  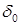(вот где сказывается аппроксимация!). Соответственно, «энтропийный шум» при назначении (2.1) или (2.4) будет больше, чем при назначении (4.2).

    К вопросу о допустимости, хотя и незначительного, но все же убывания энтропии мы еще вернемся.

    Ситуацию (4.4) для краткости будем дальше называть «звуковым приближением» для распада разрыва.

4.4. Если хотя бы одно из условий (4.4) не выполнено, придется применять более сложный алгоритм вычисления величины Р.

    Как описано в [5] на стр.110 (см. также [9], стр.168), она должна удовлетворять уравнению:

(4.7)          ,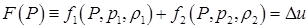

где для значений индекса k=1,2:

(4.8)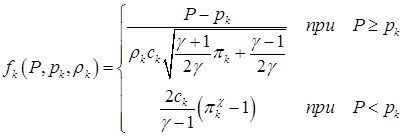

     ,      

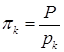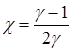
Для упрощения описания алгоритма предполагается, что 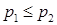 (см.[5], стр.111).

4.5. Начинаем (см. замечание ниже в разделе 5.3) с вычисления величин, определяющих «содержание» конфигурации распада разрыва.

            

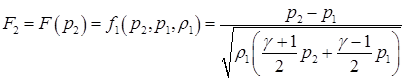
(4.9)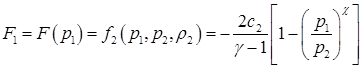    

 

         

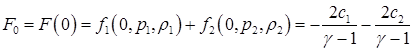
    Возможны следующие ситуации:

1⁰ если 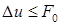 , то решения уравнения (4.7)-(4.8) не существует: образуется зона вакуума, в которой следует полагать Р =0, R =0, более подробное рассмотрение этого случая можно найти в [11];

2⁰ если 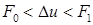 , то искомое решение находится в интервале  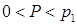, т.е. образуются две волны разрежения;

3⁰ если 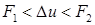 , то 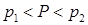 ; слева имеем ударную волну, справа – волну разрежения;

4⁰ если 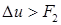 , то 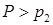 ; образуются две ударные волны.

Случаи равенства 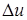 значениям  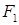или 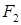 сознательно не оговариваются, чтобы при программной реализации (см. ниже раздел 5.3) охватывать их при «первой возможности».

 

4.6. Начнем с ситуации 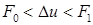 с образованием двух волн разрежения. Тогда уравнение для давления Р имеет вид:

              

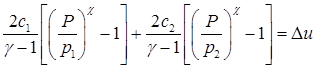
    Легко видеть, что из него явно определяется величина 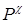 и поэтому сразу выписывается формула для его решения:

(4.10)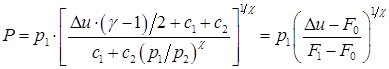     

Эта формула приведена в [5] на стр.114 и в [10] на стр.44. Можно было бы считать это исчерпывающим решением для рассматриваемой ситуации, если бы не следующее обстоятельство. При работе со сложными уравнениями состояния приходится, например, прибегать к их локальной аппроксимации двучленными уравнения состояния. Тогда параметры 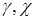 (а с ними и другие параметры) оказываются различными для индексов 1 и 2. Поэтому описанный способ становится неприемлемым и придется прибегнуть к другому алгоритму. К его описанию применительно к следующей ситуации мы и переходим. К рассматриваемой ситуации вернемся после нее.

4.7. Пусть 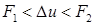 . Тогда  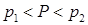и уравнение (4.7) будет содержать обе разновидности формул (4.8). Предлагается следующий алгоритм его приближенного решения. Аппроксимируем F(P) линейной функцией 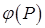, принимающей нужные значения на концах отрезка:

       ,      .

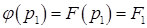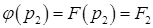Очевидно, что 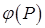 имеет вид:

               

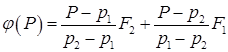
Далее решение линейного уравнения 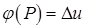 принимаем в качестве приближенного искомого решения. В качестве полезного практического совета в [10] на стр.45 рекомендуется поменять роли переменных Р и j и сразу определять обратную зависимость Р от j:

                   

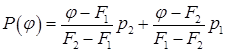
Тогда искомый приближенный корень определяется формулой:

(4.11)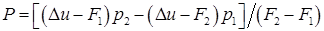        

    В [10] на стр.45 говорится, что «не представляет сложности и повысить точность интерполяции, используя значения производных 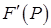 в этих же точках, при этом удобно интерполировать полиномом третьей степени зависимость ».

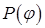К сожалению, это не совсем так. Формально действительно трудностей нет (соответствующий полином можно найти в курсах вычислительной математики). Однако он достаточно громоздок и (ввиду его единственности) должен иметь вид:

(4.12)        ,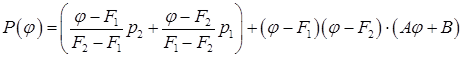

где коэффициенты А,В определяются условиями, чтобы производные этого полинома принимали заданные значения в точках на концах отрезка:

                  ,         .

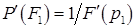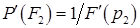Естественно, значения 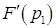 ,  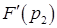для функции 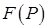, определяемой формулами (4.7)-(4.8), выписанные в [5] на стр.111, должны быть предварительно вычислены.

    Для определения А,В получается система двух линейных уравнений и, конечно, она легко решается. Но выписывать формулы мы не будем, поскольку при произвольных значениях 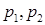 и соответствующих им значениях  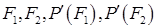гарантировать монотонность полинома (4.12) на интервале  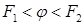не представляется возможным. А без этого его практическая ценность весьма сомнительна.

    Для описанного выше варианта линейной интерполяции вопрос о монотонности очевиден. Таким образом, весь расчет в случае 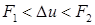 сводится к формуле (4.11).

    Напомним, что такой прием мог быть использован и в предыдущем разделе 4.6. Тогда вместо точной формулы (4.10) возникла бы приближенная, которая получается из (4.11) заменой р₂ на р₀ =0, т.е. формулой:

(4.13)          .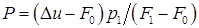

Как ни удивительно, она должна приближенно заменить (4.10).

4.8. В [5] на стр.111 были обоснованы свойства монотонности и выпуклости каждого из двух слагаемых в левой части уравнения (4.7)-(4.8). Поэтому наряду с описанной линейной интерполяцией естественный интерес представляет также интерполяция в виде параболы, проходящей через точки 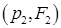, , 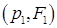, 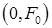причем именно в виде обратной зависимости Р(j). Тогда она определяется формулой:

(4.14)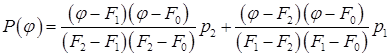    

Искомое приближенное значение Р, отвечающее значению 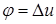, будет определяться формулой:

(4.15)    

Эта формула может использоваться на всем интервале значений 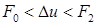. С точки зрения точности она предпочтительнее, чем (4.11) и (4.13). Исключение составляют «вырожденные» случаи:

если 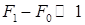, то предпочтительнее (4.11),

если 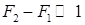, то предпочтительнее (4.13).

Условие 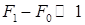 можно практически реализовывать, например, как 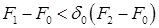, условие 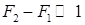, как .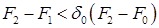

4.9. Обратимся теперь к ситуации 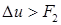. Тогда  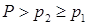и образуются две ударные волны.

    Положение осложняется тем, что Р может быть сколь угодно велико (при достаточно больших значениях 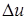). Наряду с описанием итерационного процесса решения соответствующего этому случаю уравнения

(4.16)      ,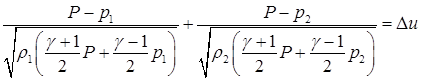

в монографии [5] на стр.113-114 и в [9] на стр.169-170 обсуждался вопрос о замене его приближенным квадратным уравнением.

Еще один интересный вариант получения квадратного уравнения предложен в [10] на стр.45. (При его описании будем иметь в виду необходимость обобщения на случай различных значений g₁ слева и g₂ справа). Запишем уравнение (4.16) так:

(4.17)          ,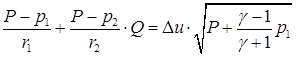

введя вспомогательные обозначения:

(4.18)       ,      ,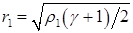

              

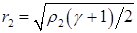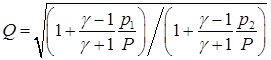
Заметим, что множитель Q близок к единице, так как р₁ и р₂ не превышают Р. Если этот множитель опустить, (4.17) превращается в уравнение

(4.19)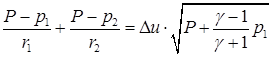    

Оно сводится к квадратному и легко решается.

Заметим далее, что точно таким же приемом получается уравнение:

(4.20)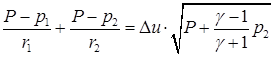    

Ввиду уже упоминавшихся свойств монотонности и выпуклости каждого из двух слагаемых в левой части уравнения (4.16) нетрудно обосновать, что (4.19) и (4.20) дают для его искомого корня приближения снизу и сверху соответственно. Можно было бы, например, использовать это для контроля точности определения корня (и, в зависимости от этого, решать вопрос, стоит ли прибегать к итерационному процессу или можно ограничиться найденным значением).

 

Выберем все же для вычисления приближенного корня уравнение (4.19), поскольку именно оно дает при Р=р₂ точное значение 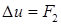, и это важно.

После возведения в квадрат, несложных преобразований и дополнительных обозначений

(4.21)       ,     ,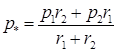

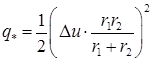получаем квадратное уравнение:

             

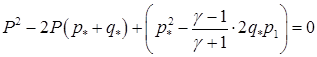
В качестве решения выбирается его больший корень

(4.22)     .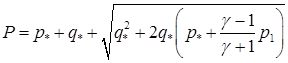

Таким образом, в рассматриваемой ситуации с двумя ударными волнами расчет приближенного значения давления Р состоит в реализации формул (4.18), (4.21) и (4.22). Кроме упомянутой выше возможности замены р₁ на р₂, заслуживает внимания с точки зрения точности замена в формуле (4.22) величины  р₁ на «взвешенное» значение 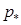. Тогда формула (4.22) принимает вид:

             .

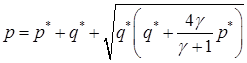    Безитерационный алгоритм приближенного вычисления давления Р описан для всех ситуаций, которые могут возникнуть при распаде разрыва (если ).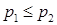

    Как уже отмечалось, его следует рассматривать как один из примеров таких алгоритмов. В частности, еще один пример описывался в [11] в расчете на более сложную ситуацию, связанную с учетом пористости среды.

 

  § 5. Некоторые замечания о практической реализации

            приближенного расчета.

 

5.1. После получения значения Р могут быть рассчитаны остальные величины, определяющие возникающую конфигурацию распада разрыва.

    Как специально отмечалось в [1] на стр.12, не следует «соблазняться» расчетом этих величин по линеаризованным формулам, а следует руководствоваться адиабатой Гюгонио (если 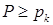) или адиабатой Пуассона (если 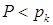) даже в случае «звукового приближения». Соответствующие формулы приведены в [5] на стр.112-113 и в [9] на стр.171-172. Для случая ударной волны мы не будем их повторять. Отметим лишь следующее важное обстоятельство. Вычисление плотностей по адиабате Гюгонио:

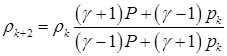                     (k=1,2)

гарантирует возрастание энтропии. По объему вычислений эти формулы не хуже, чем (1.3). Между тем эти последние в случае назначения (4.2) могут энтропию уменьшать, как следует из (4.5).

    Что касается волны разрежения, то при реализации итерационного процесса мы располагали массовыми скоростями, полученными на последней итерации. Теперь их нет, и предпочтительнее вычисления осуществлять в таком порядке.

    Прежде всего получаются значения плотностей в зонах 3 и 4:

(5.1) 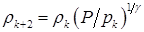      , если  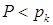  (k=1,2)

Затем – значения скоростей звука в зонах 3 и 4:

(5.2) 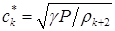        (k=1,2)

Величина U определяется, исходя из того, что в случае точного решения должно было бы быть:

            

            

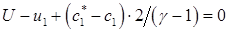
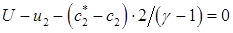
Например, так

(5.3)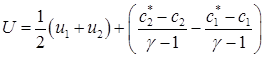     

Границы «веера характеристик», задающие волну разрежения, определяются условиями:

(5.4)       ,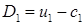    

              ,  

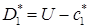
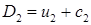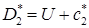
5.2. В [10] на стр.42 отмечено следующее. Хотя формулы «звукового» распада разрыва получаются для случая, когда параметры газа по обе стороны разрыва близки между собой, они приводят к устойчивому счету не только в этом случае. Несмотря на то, что вычисленные параметры P,U могут оказаться далекими от их истинных значений на соответствующих контактных поверхностях, «звуковое приближение» можно использовать гораздо чаще, чем можно было бы ожидать, исходя из предпосылок, положенных в основу его вывода.

    Отсюда следует важный для практики вывод, что безразмерный параметр 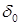 в критерии (4.4) можно назначать не так уж малым, охватывая подавляющую часть ситуаций, возникающих при практических расчетах. Возможно, при расчете некоторых задач описанный «дорогой» алгоритм вообще не будет использоваться.

5.3. Для экономии объема вычислений при программной реализации описанного алгоритма полезно иметь в виду следующее. При получении давления Р после «отказа в звуковом приближении» (4.4), есл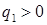и  и 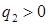, можно, не вычисляя координат «опорных» точек (4.9), сразу обратиться к случаю двух ударных волн в разделе 4.9. Есл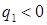и  и 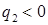, то сначала можно вычислить только F₀ и лишь убедившись, что 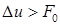, вычислять F₁, F₂ и рассматривать оставшиеся случаи.

    Далее, целью расчета является получение «больших» величин P,U,R,E на единственном луче, отвечающем значению 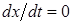 в случае неподвижной сетки (или задаваемому значению  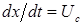, если сетка подвижна). Трудность состоит в том, что необходимо определять, в какой именно из секторов, образуемых конфигурацией распада разрыва, он попадает. Очевидно, что нет необходимости рассчитывать эту конфигурацию полностью. Например, если U <0, нет необходимости рассчитывать «левые» величины и, наоборот, если U >0 – «правые».

    В первую очередь естественно проверять возможности, требующие меньшего объема вычислений. Самым «трудоемким» является получение величин в случае попадания внутрь сектора, занимаемого волной разрежения (см. [5], стр.120 или [9], стр.171).

    Заметим, что «протяженность» сектора, охватываемого левой волной разрежения, определяется формулой:

                

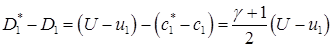
    Аналогично, для правой волны разрежения:

                

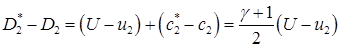
Если эти величины малы, можно внутрь такого сектора и не «влезать», а ограничиться формулами типа линейной интерполяции.

    Однако в случае сильных волн разрежения выбор соответствующего луча становится существенным. Об этом свидетельствует и опыт расчетов и необходимость довольно громоздкой меры для обеспечения сходимости итерационного процесса, описанной в [4] (см. также [5], стр.110).

5.4. Достоинством описанного приближенного алгоритма является то, что он во всех случаях качественно правильно описывает возникающие конкретные конфигурации распада разрыва. Учитывая, что использоваться будет лишь небольшая часть информации в виде «больших» величин на одном луче, на основе которых будут вычисляться газодинамические потоки, можно надеяться, что и количественно его результаты вполне приемлемы.

5.5. В [1] на стр.18 отмечалась особая роль точного расчета распада разрыва как универсального инструмента для расчета движения границ физических областей, например, разделяющих области с совершенно разными парамет-рами. По нашему мнению, и описанный приближенный безитерационный метод, как правило, вполне может претендовать на такую роль.

5.6. Для успешного исполнения этой роли, а также для практической возможности использования описанного метода не только для уравнения состояния (1.1), но и для более сложных случаев, требуется его модификация. В § 8 работы [1] рассматривались некоторые из возникающих при этом проблем.

    Рассмотрим важный для практики расчетов случай, когда газодинамические параметры с индексами 1 и 2 удовлетворяют двучленным уравнениям состояния со своими параметрами:

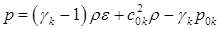                              (k=1,2)

Это отражается в формулах для скорости звука и энтропии:

                  ,    

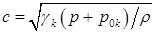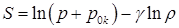
Соответственно должны быть изменены формулы (1.9)-(1.11) и формулы (4.1), (4.4). Например, последняя должна быть заменена на следующую:

                  ,    

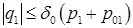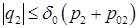
    В основном уравнении (4.7)-(4.8) должна быть сделана заме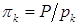на  на 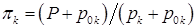;  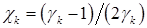должны заменить c. Это приводит к столь многочисленным и громоздким изменениям в формулах § 4 и § 5, что мы ограничимся только наиболее важными расчетными формулами.

    Прежде всего это касается формул (4.9) для «опорных» точек, которые должны быть заменены на следующие:

             

             

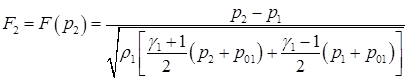
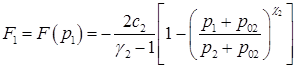
Что касается последней из формул (4.9), то в ней Р= 0 должно быть заменено на 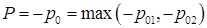. Поскольку вакуума достигает первой либо левая (если 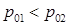), либо правая среда (если 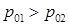), формула для F₀ принимает следующий вид:

 

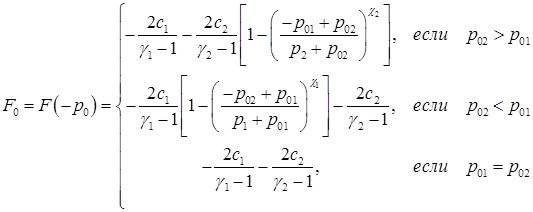
    Применение формулы (4.10), как уже отмечалось в разделе 4.6, в случае 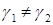,  становится невозможным, и ее придется заменить приближенной.

Поскольку 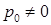, такая приближенная формула (4.13) должна быть заменена на аналогичную (4.11):

       

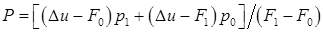
Усложняется уравнение параболы (4.14), в котором добавляется еще одно слагаемое

.

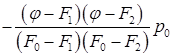Соответственно изменяется и формула (4.15):

      

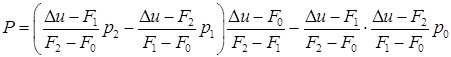
В разделе 4.9 основное «рабочее» уравнение (4.19) должно быть заменено на следующее:

      

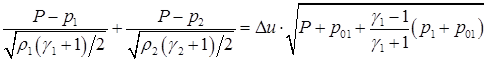
Поэтому изменения в расчетных формулах таковы.

Формулы (4.18) заменяются на

           ,      ,

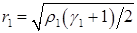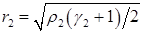а в формуле (4.22) слагаемое 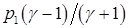 заменяем на

         .

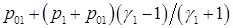Корректируются также формулы (5.1) и (5.2):

          ,         

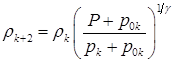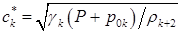
    Подчеркнем, что перечислены изменения не всех, а только расчетных формул алгоритма для случая .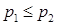

5.7. В случае сложных уравнений состояния (не двучленного вида) на практике для решения задачи о распаде разрыва широко используется прием замены их локальной аппроксимацией соответствующими двучленными уравнениями состояния (своими для каждой из зон 1 или 2). Именно поэтому такой случай стал предметом специального рассмотрения в предыдущем разделе.

    Однако, как отмечалось в [1] на стр.25, такой прием не является универсальным. Возможность расчета распада разрыва для сложных уравнений состояния рассматривались, например, в [12] и в [9] на с.175-176.

    Наконец, уместно упомянуть о достаточно универсальном подходе к решению задачи о распаде разрыва в случае сколь угодно сложных уравнений состояния, изложенном в небольшой монографии [13]. Рассмотрение упомянутых работ выходит за рамки настоящей.

 

Снова об энтропии.

 

6.1. Вопрос об энтропийных эффектах и «энтропийных следах», появляющихся в численных расчетах газодинамических задач, издавна был одним из дискуссионных. В качестве примера можно привести цитату из [14]: «По нашему мнению, для расчета адиабатических течений могут применяться лишь такие разностные схемы, в которых изменение энтропии из-за погрешностей аппроксимации уравнений при малых значениях 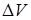 (приращение удельного объема 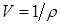) хотя бы не превосходит физического изменения энтропии на слабых ударных волнах».

Как известно (см., напр., [15]), на слабых ударных волнах приращение энтропии 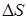 пропорционально кубу приращения удельного объема: .

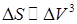В [14] рассматривались разностные схемы для уравнений газовой динамики в переменных Лагранжа в адиабатическом приближении, т.е. при отсутствии вязкости, тепловых потоков и источников энергии. Проведенные в ней исследования показали, что такие разностные схемы, в которых вычислительные источники производства энтропии при расчете гладких течений по порядку величины не превосходят физических источников, существуют. В этих схемах погрешности аппроксимации суть величины порядка 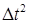 ( 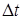 - шаг по временной координате).

6.2. Схема С.К.Годунова и в случае лагранжевых, и в случае эйлеровых переменных таковой не является, поскольку для нее погрешность аппроксимации имеет порядок 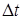. Именно поэтому и возникает желание порядок аппроксимации повысить. Эту цель ставят перед собой некоторые из авторов, предлагающих схемы «типа Годунова». Поскольку при этом обычно используется задача о распаде разрыва, естественно, чтобы она давала решение, для которого «вычислительный шум», не превосходит создаваемый реальными физическими процессами, например, слабыми ударными волнами.

Точный расчет распада разрыва такими свойствами обладает. Это уже неоднократно отмечалось, и мы не будем на этом останавливаться.

Что касается описанного приближенного расчета распада разрыва, то приращение энтропии 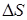 имеет не третий, а второй порядок (см. выше раздел 4.3). Этого вполне достаточно для схемы первого порядка, каковой является метод Годунова, но может оказаться недостаточным, если речь пойдет о достижении более высокого порядка аппроксимации при расчете гладких течений.

 

6.3. В связи с обсуждаемым вопросом уместно процитировать также стр.12 работы [16]: «При расчетах сильных изэнтропических волн разрежения по моей [С.К.Годунова] схеме наблюдается значительный рост энтропии, который постоянно служил источником неприязни к результатам разностных расчетов. Существенное снижение этого эффекта было замечено только, когда приступили к расчету двумерных задач… Двумерные программы, использующие эйлеровы координаты, приводят к существенно меньшему «паразитическому» повышению энтропии в волнах разрежения. Причина этого явления состоит в том, что лагранжевы координаты (даже в простейшем одномерном случае) непригодны для формулировки понятия «обобщенные решения» уравнений гидродинамики. Эти уравнения допускают при некоторых начальных данных появление полостей, не заполненных средой, - зон вакуума, которые в лагранжевых координатах изображаются наличием у решения особенностей типа дельта-функции. Такие особенности у обобщенных решений обычно не предусматриваются и при разностной аппроксимации очень плохо моделируются…»

 

6.4. Отметим, что в настоящей работе, как и в [1], обращается внимание на необходимость контроля энтропии с тем, чтобы не допустить неоправданного ее занижения в газодинамических расчетах. В некотором смысле это противоречит «борьбе» за минимизацию энтропийных эффектов, порождаемых разностной схемой. На первый план выдвигаются интересы гарантированного получения физически реализуемых течений.