2020-01-14
160
Посевная площадь представляет основную форму сельскохозяйственного использования пашни.
По данным Приложения 14 определим состав и структуру посевной площади.
Общая посевная площадь сельскохозяйственных культур по категориям хозяйств текущего года в хозяйствах всех категорий, по данным Приложения 14, составила 84,6 млн.гектаров.
По таблице видно, что в состав посевной площади входят: зерновые культуры, технические культуры, картофель и овощебахчевые культуры, кормовые культуры.
2. Группировка центральных районов России по размеру валового сбора зерна (производства молока)
Из Приложения 1 и 7 за 2000 год имеются данные о валовом сборе зерна и производстве молока по Центральному, Южно федеральному и Приволжскому округам РФ.
Группировка по Центральному федеральному округу РФ за 2000 год.
Таблица2
| Центральный федеральный округ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| валовый сбор зерна | 1347 | 395,7 | 233,8 | 1720,7 | 169 | 147,0 | 147,4 | 1400,6 | 921,6 | ||
| Производство молока | 233,2 | 234,1 | 301,4 | 313,7 | 338,0 | 344,2 | 351,6 | 357,3 | 390,1 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
| Центральный федеральный округ | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| ||
| валовый сбор зерна | 341,4 | 1397,6 | 689,2 | 189,0 | 1025,0 | 174,5 | 641,5 | 153,7 |
| ||
| Производство молока | 433,9 | 441,8 | 462,0 | 482,0 | 484,0 | 604,8 | 758,8 | 1024,9 |
| ||
Для построения группировки по размеру валового сбора зерна и производства молока определим вначале минимальное и максимальное значение группировочного признака, которым является производство молока: Xmin = 233, 2; Xmax = 1024,9 млн.т
Затем построим интервальный ряд. Для этого группировочный признак разобьем на три интервала, величина которого определяется по формуле:
h=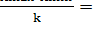 
= 263,9
Используя величину интервала группировочного признака, определим интервалы групп и составим вспомогательную таблицу 2.1
Вспомогательная таблица для сводки данных по группам округов Таблица 2.1
| № групп | Группа регионов по производству молока млн.т | Валовый сбор зерна | Производство молока | Центральный федеральный округ |
| 1 | 233, 2 - 497,1 | 1347; 395,7; 233,8; 1720,7; 169; 147,0; 147,4;1400,6;921,6; 341,4;1397,6;689,2; 189,0; 1025,0 | 233,2; 234,1; 301,4; 313,7;338,0;344,2;351,6; 357,3; 390,1; 433,9; 441,8; 462,0;482,0;484,0 |
14 |
| Итого по первой группе | 10125 | 5167,3 | ||
| 2 | 497,2 - 761 | 174,5; 641,5 | 604,8; 758,8 |
2 |
| Итого по второй группе | 816 | 1363,6 | ||
| 3 | 762 – 1024,9 | 153,7 | 1024,9 |
1 |
| Итого по третей группе | 153,7 | 1024,9 | ||
| Всего | 11094,7 | 7555,8 | 17 | |
По итоговым данным валового сбора зерна и производства молока рассчитаем их среднее значение по каждой из групп с помощью средней арифметической простой. Группировочная таблица будет иметь вид (таб.2.3)
3. Структурные средние, показатели вариации (по результам группировоки (п.2). Построить график.
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
,
где XMe – нижняя граница медианного интервала;
hMe – его величина;
(Sum m)/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
SMe-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
В нашем примере могут быть получены даже три медианных значения – исходя из признаков количества предприятий, объема продукции и общей суммы затрат на производство:
Таким образом, у половины предприятий уровень себестоимость единицы продукции превышает 125,19 тыс. руб., половина всего объема продукции производится с уровнем затрат на изделие больше 124,79 тыс. руб. и 50 % общей суммы затрат образуется при уровне себестоимости одного изделия выше 125,07 тыс. руб. Заметим также, что наблюдается некоторая тенденция к росту себестоимости, так как Ме2 = 124,79 тыс. руб., а средний уровень равен 123,15 тыс. руб.
При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как
,
где ХMo – нижнее значение модального интервала;
mMo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
mMo-1 – то же для интервала, предшествующего модальному;
mMo+1 – то же для интервала, следующего за модальным;
h – величина интервала изменения признака в группах.
Для нашего примера можно рассчитать три модальных значения исходя из признаков числа предприятий, объема продукции и суммы затрат. Во всех трех случаях модальный интервал один и тот же, так как для одного и того же интервала оказываются наибольшими и число предприятий, и объем продукции, и общая сумма затрат на производство:
Таким образом, чаще всего встречаются предприятия с уровнем себестоимости 126,75 тыс. руб., чаще всего выпускается продукция с уровнем затрат 126,69 тыс. руб., и чаще всего затраты на производство объясняются уровнем себестоимости в 123,73 тыс. руб.
Показатели вариации
Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.
Для измерения вариации в статистике применяют несколько способов.
Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака:
H=Xmax - Xmin.
Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной:
(Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.)
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
Дисперсия признака (s2) определяется на основе квадратической степенной средней:
.
Показатель s, равный 
, называется средним квадратическим отклонением.
В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.
Если вариация оценивается по небольшому числу наблюдений, взятых из неограниченной генеральной совокупности, то и среднее значение признака определяется с некоторой погрешностью. Расчетная величина дисперсии оказывается смещенной в сторону уменьшения. Для получения несмещенной оценки выборочную дисперсию, полученную по приведенным ранее формулам, надо умножить на величину n / (n - 1). В итоге при малом числе наблюдений (< 30) дисперсию признака рекомендуется вычислять по формуле
.
Обычно уже при n > (15÷20) расхождение смещенной и несмещенной оценок становится несущественным. По этой же причине обычно не учитывают смещенность и в формуле сложения дисперсий.
Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле
,
где n – объем выборки; s2 – дисперсия признака, рассчитанная по данным выборки.
Величина 
носит название средней ошибки выборки и является характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины. Показатель средней ошибки используется при оценке достоверности результатов выборочного наблюдения.
