Разрывные функции и их производные

    XX - XI век находит много конструктивных решений для того, что казалось невозможным в XIX веке. Так дельта-функция решает вопрос о производной в точке разрыва (в частности, для разрыва, имеющего вид конечного скачка).

    Рассмотрим интеграл функции δ(x) в зависимости от его верхнего предела, то есть функцию

. (12)

График этой функции имеет вид «ступеньки» (рис.8). Пока x<0, область интегрирования в формуле (12) целиком находится там, где δ(x)=0. Следовательно, θ(x)=0  при x<0. Если же x>0, то при интегрировании включается окрестность начала координат, где . С другой стороны, так как при x>0 также δ(x)=0, то значение интеграла не изменяется, когда верхний предел меняется от 0,1 до 1, или до 10, или до ∞. Следовательно, при x>0 имеем

как и показано на рис.8.

    Таким образом, с помощью дельта-функции сконструирована простейшая разрывная функция θ(x) такая, что при x<0, θ(x)=0, а в области x>0, θ(x)=1. При x=0, θ терпит разрыв от 0 до 1.

    Не зная дельта-функции, приходится говорить, что производную нельзя находить там, где функция разрывна. Мы построили разрывную функцию θ(x). По теореме о существовании первообразной для ограниченной функции, имеющей конечное или счетное число точек разрыва, общее правило связи между интегралом и производной имеет вид:              

 .

Тогда .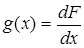

Применим его к выражению (12), получим

.

Значит, для производной разрывной функции не надо делать исключений: просто в точке разрыва производная равна «особенной» функции – дельта-функции Дирака.

    Производная разрывной функции определяется следующим образом:

f’(x)={f’(x)}+[f_x0 ]δ(x – x₀),

где f_x0 – величина разрыва в точке x₀,

{f’(x)} – производная везде, кроме точки x₀.

Благодаря дельта-функции Дирака можно найти производные в более сложных случаях.