Свойство 1. Метризуемое пространство хаусдорфово.
Доказательство. Пусть  . Возьмем
. Возьмем 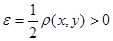 . Докажем, что
. Докажем, что  .
.
Предположим, что  , тогда существует
, тогда существует  , т.е.
, т.е.  и
и  . Тогда,
. Тогда,  . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  .
.
Следствие. Метризуемое пространство является  - пространством.
- пространством.
Определение. Расстоянием от точки  до множества
до множества 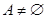 в метрическом пространстве называется
в метрическом пространстве называется  .
.
Утверждение 2. Пусть множество  фиксировано; тогда функция
фиксировано; тогда функция  , сопоставляющая каждой точке
, сопоставляющая каждой точке  расстояние
расстояние 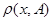 , непрерывна на пространстве
, непрерывна на пространстве  .
.
Доказательство. Воспользуемся определением непрерывности: функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если  .
.
Из неравенства  , где
, где  , получаем
, получаем  . Аналогично
. Аналогично  . Из полученных неравенств следует
. Из полученных неравенств следует  .
.
Для произвольного  возьмем
возьмем  . Тогда из неравенства
. Тогда из неравенства  следует
следует  . Непрерывность
. Непрерывность  доказана.
доказана.
Лемма.  – замкнутое множество в метрическом пространстве
– замкнутое множество в метрическом пространстве  . Для любого
. Для любого  расстояние от
расстояние от  до множества
до множества  положительно.
положительно.
Доказательство.
Множество  замкнуто, отсюда следует, что множество
замкнуто, отсюда следует, что множество  - открыто. Так как точка
- открыто. Так как точка  принадлежит открытому множеству
принадлежит открытому множеству  , то существует такое
, то существует такое  , что
, что  . Так как
. Так как  , то
, то 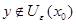 для некоторого
для некоторого  . Поэтому
. Поэтому 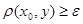 для любого
для любого  . Следовательно,
. Следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Свойство 2. Метризуемое пространство нормально.
Доказательство. По доказанному метризуемое пространство является
 -пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества
-пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества  и
и  имеют непересекающиеся окрестности.
имеют непересекающиеся окрестности.
Так как  и множество
и множество  замкнуто по условию, то для любого
замкнуто по условию, то для любого  по лемме
по лемме  .
.
Обозначим 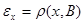 и
и  для произвольных
для произвольных  и
и  .
.
Множества  и
и  открыты как объединения открытых шаров в
открыты как объединения открытых шаров в  и содержат соответственно множества
и содержат соответственно множества  и
и  .
.
Следовательно,  - окрестность множества
- окрестность множества  ,
,  - окрестность множества
- окрестность множества  .
.
Докажем, что  .
.
Предположим, что  , то есть
, то есть  . Тогда из условия
. Тогда из условия  следует, что
следует, что  для некоторого
для некоторого 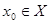 . Отсюда
. Отсюда 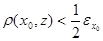 .
.
Аналогично получаем  для некоторого
для некоторого 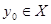 . Для определенности пусть
. Для определенности пусть  . Тогда
. Тогда 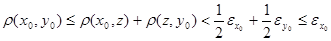 .
.
Получаем 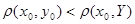 , для некоторой точки
, для некоторой точки  , что невозможно в силу определения расстояния от точки до множества.
, что невозможно в силу определения расстояния от точки до множества.
Следовательно 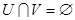 . Таким образом,
. Таким образом,  является
является  -пространством, а, значит, нормальным пространством. Теорема доказана.
-пространством, а, значит, нормальным пространством. Теорема доказана.
Свойство 3. В метризуемом пространстве  выполняется первая аксиома счетности.
выполняется первая аксиома счетности.
Доказательство. Пусть  - произвольное открытое множество, содержащее точку
- произвольное открытое множество, содержащее точку  . Так как открытые шары образуют базу топологии метрического пространства, то
. Так как открытые шары образуют базу топологии метрического пространства, то  содержится в
содержится в  вместе с некоторым открытым шаром, то есть
вместе с некоторым открытым шаром, то есть  для некоторых
для некоторых  и
и  . По утверждению 1 найдется такое
. По утверждению 1 найдется такое  , что
, что 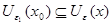 .
.
Возьмем  , для которого
, для которого  . Тогда
. Тогда  . Таким образом открытые шары
. Таким образом открытые шары  ,
,  образуют определяющую систему окрестностей точки
образуют определяющую систему окрестностей точки 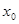 . Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.
. Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.
Определение. Множеством типа 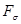 или просто
или просто 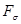 - множеством пространства
- множеством пространства  называется всякое множество
называется всякое множество 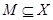 , являющееся объединением счетного числа замкнутых (в
, являющееся объединением счетного числа замкнутых (в  ) множеств.
) множеств.
Определение. Множеством типа  или просто
или просто  - множеством пространства
- множеством пространства  называется всякое множество
называется всякое множество 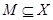 , являющееся пересечением счетного числа открытых (в
, являющееся пересечением счетного числа открытых (в  ) множеств.
) множеств.
Очевидно, что множества типа 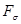 и
и  являются взаимно дополнительными друг для друга.
являются взаимно дополнительными друг для друга.
Определение. Нормальное пространство, в котором всякое замкнутое множество является множеством типа  , называется совершенно нормальным.
, называется совершенно нормальным.
Утверждение 3. Нормальное пространство является совершенно нормальным тогда и только тогда, когда всякое открытое множество, принадлежащее этому пространству, является множеством типа 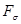 .
.
Свойство 4. Метризуемое пространство совершенно нормально.
Доказательство. Пусть  - непустое замкнутое множество в
- непустое замкнутое множество в  . Тогда
. Тогда 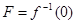 для непрерывной функции
для непрерывной функции 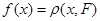 (непрерывность ее установлена в утверждении 2). Обозначим
(непрерывность ее установлена в утверждении 2). Обозначим  , множества
, множества  открыты в
открыты в  как прообразы открытых множеств при непрерывном отображении. Докажем, что
как прообразы открытых множеств при непрерывном отображении. Докажем, что  .
.
Пусть 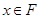 , тогда
, тогда  . Так как
. Так как  для любого
для любого  , то
, то  для любого
для любого  . Отсюда
. Отсюда  .
.
Обратно. Пусть  , тогда
, тогда  для любого
для любого  . Отсюда
. Отсюда  для любого
для любого  , поэтому
, поэтому  для любого
для любого  , тогда
, тогда  , значит
, значит  . Таким образом множество
. Таким образом множество  является множеством типа
является множеством типа  .
.
Определение. Множество  всюду плотно в
всюду плотно в  , если любое непустое открытое в
, если любое непустое открытое в  множество содержит точки из
множество содержит точки из  .
.
Определение. Топологическое пространство  называется сепарабельным, если оно имеет счетное всюду плотное подмножество.
называется сепарабельным, если оно имеет счетное всюду плотное подмножество.
Определение. Семейство γ открытых в  множеств образуют покрытие пространства
множеств образуют покрытие пространства  , если
, если  содержится в объединении множеств этого семейства.
содержится в объединении множеств этого семейства.
Определение. Топологическое пространство  называется финально компактным, если из любого его открытого покрытия можно выделить счетное подпокрытие.
называется финально компактным, если из любого его открытого покрытия можно выделить счетное подпокрытие.
Свойство 5. Для метризуемого пространства  следующие условия эквивалентны:
следующие условия эквивалентны:
1)  сепарабельно,
сепарабельно,
2)  имеет счетную базу,
имеет счетную базу,
3)  финально компактно.
финально компактно.
Доказательство. 
Пусть  - счетное всюду плотное множество в
- счетное всюду плотное множество в  ,
,  - метрика в
- метрика в  . Множество окрестностей
. Множество окрестностей 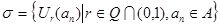 счетно. Докажем, что
счетно. Докажем, что  - база топологии в
- база топологии в  . Пусть
. Пусть  - произвольное открытое в
- произвольное открытое в  множество,
множество,  . Тогда
. Тогда  для некоторого
для некоторого  . Рассмотрим рациональное число
. Рассмотрим рациональное число  , для которого
, для которого  и точку
и точку 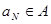 , для которой
, для которой  .
.
Докажем, что  . Пусть
. Пусть  . Так как
. Так как  , то
, то  . Тогда
. Тогда  . Таким образом, для произвольного
. Таким образом, для произвольного  и открытого множества
и открытого множества  нашелся элемент из
нашелся элемент из  , такой, что
, такой, что  . Следовательно
. Следовательно  - база топологии.
- база топологии.
 Пусть
Пусть  - счетная база в
- счетная база в  . Рассмотрим произвольное открытое покрытие множества
. Рассмотрим произвольное открытое покрытие множества 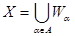 ,
,  - открыты для любого
- открыты для любого  (
( - индексное множество). Для любого
- индексное множество). Для любого  существует
существует  , для которого
, для которого  . Так как
. Так как  - база, то найдется такое
- база, то найдется такое  , что
, что 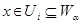 . Тогда
. Тогда  . Поскольку база
. Поскольку база  счетна, то
счетна, то  покрывается счетным числом соответствующих множеств
покрывается счетным числом соответствующих множеств  . Таким образом,
. Таким образом,  - финально компактно.
- финально компактно.
 Для каждой точки
Для каждой точки  рассмотрим окрестности
рассмотрим окрестности  , которые образуют покрытие пространства
, которые образуют покрытие пространства  . В силу финальной компактности
. В силу финальной компактности  из этого покрытия можно выделить счетное подпокрытие
из этого покрытия можно выделить счетное подпокрытие  . В каждом из этих множеств выберем точку
. В каждом из этих множеств выберем точку  . Множество точек
. Множество точек 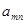 счетно, докажем, что оно плотно в
счетно, докажем, что оно плотно в 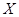 . Пусть
. Пусть  - произвольное открытое множество в
- произвольное открытое множество в  ,
,  , тогда
, тогда  для некоторого
для некоторого 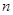 . Существует элемент подпокрытия
. Существует элемент подпокрытия  . Тогда
. Тогда  , то есть любое непустое открытое множество в
, то есть любое непустое открытое множество в  содержит точку этого множества. Что и требовалось доказать.
содержит точку этого множества. Что и требовалось доказать.
Определение. Диаметром непустого множества  в метрическом пространстве
в метрическом пространстве  называется точная верхняя грань множества всех расстояний между точками множества
называется точная верхняя грань множества всех расстояний между точками множества  и обозначается
и обозначается  .
.
 .
.
Если  , то множество
, то множество  называют неограниченным.
называют неограниченным.
Определение. Метрика  метрического пространства
метрического пространства 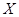 называется ограниченной, если
называется ограниченной, если  .
.
Свойство 6. Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.
Доказательство. Пусть метрика  порождает топологию топологического пространства
порождает топологию топологического пространства 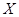 . Положим
. Положим  для любых
для любых  .
.
Докажем следующее:
1. 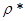 -метрика на
-метрика на 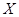 ;
;
2. метрики 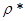 и
и  эквивалентны;
эквивалентны;
3. 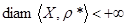 .
.
1. Проверим выполнимость аксиом.
1) 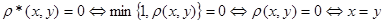 ;
;
2) 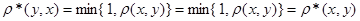 ;
;
 : Докажем, что
: Докажем, что  .
.
Известно, что 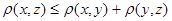 .
.
· Если  и
и  , то
, то  и
и  , тогда
, тогда  . Так как
. Так как  , то
, то  .
.
· Если  или
или  , то
, то  , а
, а  , тогда
, тогда  .
.
2. Пусть  - топология, порожденная метрикой
- топология, порожденная метрикой  , а
, а  - топология, порожденная метрикой
- топология, порожденная метрикой  . Докажем, что
. Докажем, что  .
.
Пусть  - открытое множество в
- открытое множество в  , докажем, что множество
, докажем, что множество 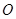 открыто в
открыто в  . Для любого
. Для любого  существует
существует  такое, что
такое, что  . Можно считать, что
. Можно считать, что  . Тогда
. Тогда  является окрестностью в
является окрестностью в  того же радиуса
того же радиуса  . Следовательно,
. Следовательно, 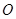 открыто в топологии
открыто в топологии  .
.
В обратную сторону доказательство проводится аналогично.
Из всего выше сказанного следует, что метрики  и
и 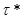 эквивалентны.
эквивалентны.
3. Из формулы  следует, что
следует, что  для любых
для любых  . Отсюда
. Отсюда  .
.
Определение. 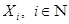 - топологические пространства,
- топологические пространства,  . Тихоновским произведением топологических пространств
. Тихоновским произведением топологических пространств 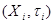 называется топологическое пространство
называется топологическое пространство  , в котором базу топологии образуют множества
, в котором базу топологии образуют множества  , где
, где  открыто в
открыто в  для любого
для любого  и
и  для всех индексов кроме конечного их числа.
для всех индексов кроме конечного их числа.
Свойство 7. Произведение счетного числа метризуемых пространств метризуемо.
Доказательство. Пусть 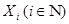 - метризуемые топологические пространства. По лемме на каждом множестве
- метризуемые топологические пространства. По лемме на каждом множестве  существует ограниченная метрика
существует ограниченная метрика  соответственно.
соответственно.
Рассмотрим  .
.
Покажем:
1.  является метрикой на
является метрикой на 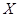 и
и  .
.
2. топология, порожденная метрикой  , совпадает с топологией произведения пространств
, совпадает с топологией произведения пространств 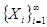 .
.
1. Проверим выполнимость аксиом метрики.
1)  (так как
(так как  - метрика по условию).
- метрика по условию).
2)  ,
,  .
.
Так как  (
( -метрика по условию), то
-метрика по условию), то  , тогда
, тогда  .
.
3) Докажем, что  .
.
 ,
,  ,
,  . Но так как выполняется неравенство
. Но так как выполняется неравенство  , то будет выполняться неравенство:
, то будет выполняться неравенство:
 , тогда
, тогда  .
.
Теперь докажем, что  .
.
 , где
, где  геометрическая прогрессия, а
геометрическая прогрессия, а  , тогда
, тогда  .
.
2. 1) Покажем, что каждое множество  , открытое в топологии, индуцированной метрикой
, открытое в топологии, индуцированной метрикой  , открыто и в топологии произведения.
, открыто и в топологии произведения.
Рассмотрим произвольную точку  . Существует такое
. Существует такое  , что
, что 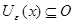 . Далее достаточно найти положительное число
. Далее достаточно найти положительное число  и открытые множества
и открытые множества  , такие, что
, такие, что 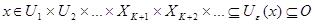 .
.
Пусть  - положительное целое число, удовлетворяющее условию:
- положительное целое число, удовлетворяющее условию:
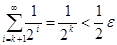 .
.
Для  положим
положим 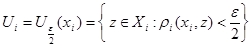 и
и  для
для  .
.
Для каждой точки 
 . Рассмотрим полученные суммы. Так как
. Рассмотрим полученные суммы. Так как  , где
, где  , то
, то  . Так как
. Так как  для любых
для любых  , то
, то  . Тогда
. Тогда  , т.е.
, т.е. 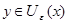 . Таким образом
. Таким образом  . Следовательно, множество
. Следовательно, множество  открыто в тихоновской топологии произведения.
открыто в тихоновской топологии произведения.
2) Пусть множество  открыто в топологии произведения. Докажем, что оно открыто в топологии, порожденной метрикой
открыто в топологии произведения. Докажем, что оно открыто в топологии, порожденной метрикой 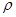 .
.
Требуется доказать, что для любой точки  найдется такое
найдется такое  , что
, что  .
.
Так как множество  открыто в топологии произведении, то
открыто в топологии произведении, то  для некоторого множества
для некоторого множества 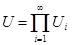 , где
, где 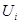 - открыто в
- открыто в  и
и  для любого
для любого 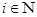 и
и  для всех индексов
для всех индексов  кроме конечного их числа. Поскольку
кроме конечного их числа. Поскольку  и
и 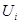 открыто в
открыто в  , то
, то  для конечного числа индексов, для которых
для конечного числа индексов, для которых  . Пусть
. Пусть  - наименьший из этих значений
- наименьший из этих значений  . Докажем, что
. Докажем, что  . Возьмем произвольное
. Возьмем произвольное  . Тогда
. Тогда  . Отсюда
. Отсюда  для любого
для любого  . Это означает, что
. Это означает, что  для любого
для любого 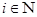 . Получили
. Получили  . Следовательно, множество
. Следовательно, множество  открыто в топологии, индуцируемой метрикой
открыто в топологии, индуцируемой метрикой  . Теорема доказана.
. Теорема доказана.
 2020-01-14
2020-01-14 202
202