Глава III. Примеры метризуемых и неметризуемых пространств

1. Дискретное топологическое пространство.

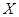 - произвольное непустое множество. Открытым назовем любое подмножество в 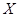. Очевидно, при этом выполнены все аксиомы топологического пространства. Рассмотрим  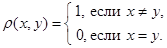 Для любого  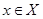множество  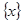открыто, так как 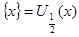. Следовательно, открыто и любое подмножество в  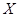как объединение одноэлементных множеств. Вывод: дискретное топологическое пространство – метризуемо.

2. Двоеточия.

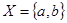. Рассмотрим топологии на .

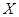1) 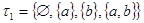 - простое двоеточие.

2) 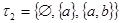 - связное двоеточие.

3) 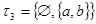 - слипшееся двоеточие.

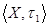 - метризуемо, так как топология  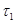- дискретная.

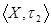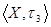,  - неметризуемы, так как не являются хаусдорфовыми.

3. Стрелка ().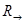

В 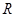 открытыми назовем  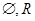и множества вида 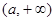, где 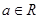. Очевидно, при этом выполнены все аксиомы топологического пространства. Топологическое пространство  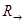не является хаусдорфовым, а значит неметризуемо.

4. Окружности Александрова (пространство ).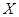

Открытые множества в :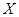

первого рода: интервал на малой окружности 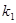 плюс его проекция на большую окружность 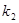, из которой выброшено конечное число точек.

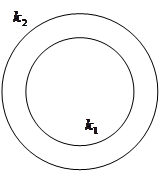второго рода: каждая точка на большой окружности открыта.

1. Множество 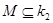 замкнуто в  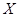тогда и только тогда, когда  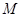- конечно.

Доказательство. Очевидно, что любое конечное множество 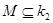 замкнуто как дополнение открытого. Пусть  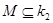и 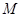  - бесконечно. Докажем, что  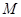- незамкнуто.

Так как 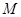  - бесконечно, то оно содержит счетное подмножество, которое можно рассмотреть как последовательность точек, принадлежащих 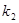. Эта последовательность ограничена в 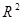, по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность. Так как  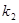замкнуто в 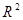, то предел этой последовательности 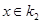. Пусть  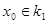- точка, для которой  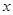является проекцией на 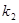. Возьмем произвольное открытое в  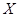множество 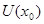, содержащее точку 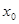. Тогда исходя из структуры открытых множеств первого рода получаем, что  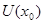содержит бесконечно много точек множества 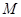, т.е.  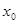является предельной точкой множества 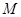. При этом 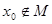. Следовательно,  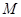- незамкнуто.

2. Множество 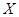 не совершенно нормально.  

Доказательство. Пусть дуга 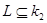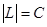. Множество  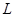открыто, как объединение открытых одноэлементных множеств. Замкнутыми в  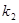являются по доказанному лишь конечные множества. Но счетное объединение конечных множеств счетно. Следовательно  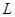открыто и не является множеством типа 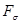. Таким образом множество  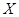неметризуемо.