2020-01-14
219
Уравнение линейной регрессии имеет вид: y = a + bx + e [2].
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических ŷx минимальна, то есть:
.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
.
Из этой системы следуют формулы:
.
Для расчета множественной линейной регрессии данные представляются в матричной форме [6]:
Y = Xb + e,
или
,
где матрица X называется регрессионной матрицей, вектор b — неизвестные параметры, подлежащие оцениванию, а столбец e — ошибки.
Пользуясь МНК, имеем:
.
В результате получаем выражение для оценки вектора b:
.
Соответственно, появляется модель, связывающая экспериментальные данные:
.
Как для моделей парной, так и для множественной регрессии справедливы статистические оценки, описанные в таблице 7 [2]:
|
|
|
Таблица 7
| Название характеристики | Обозначение | Формула | Описание |
| Полная дисперсия | TSS | 
| Общая сумма квадратов отклонений зависимой переменной от ее выборочного значения |
| Часть дисперсии, необъясненная регрессией | ESS | 
| Необъясненная сумма квадратов отклонений |
| Часть дисперсии, объясненная регрессией | RSS | 
| Объясненная сумма квадратов отклонений |
| Коэффициент детерминации | R2 | RSS/TSS | — |
| F-статистика (критерий Фишера) | F | 
| Оценка качества уравнения регрессии. Состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического F (где n – число единиц совокупности, m — число параметров при переменных x) и табличного (критического) Fтабл. Fтабл — это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α — вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равным 0,05 или 0,01. Если Fтабл < F, то H0 — гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Иначе — |
Продолжение таблицы 7
| Название характеристики | Обозначение | Формула | Описание |
| признается статистическая незначимость, ненадежность уравнения регрессии. | |||
| Средняя ошибка аппроксимации | 
| 
| Среднее отклонение расчетных данных от фактических |
Для расчета доверительных интервалов параметров линейной регрессии применяются статистически оценки, приведенные в таблице 8:
|
|
|
Таблица 8
| Название характеристики | Обозначение | Формула | Описание |
| Случайная ошибка параметра a линейной регрессии | ma |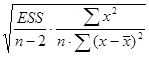 
| — |
| Случайная ошибка параметра b линейной регрессии | mb | 
| — |
| t-критерий Стьюдента для параметра а | ta | 
| Рассчитывается для оценки статистической значимости коэффициентов регрессии. Выдвигается гипотеза H0 о случайной природе показателей, то есть о незначимом их отличии от нуля. Сравнивая фактическое и табличное (критическое) значения для заданного уровня значимости, принимаем или отвергаем выдвинутую гипотезу: если |
| t-критерий Стьюдента для параметра b | tb | 
|
Продолжение таблицы 8
| Название характеристики | Обозначение | Формула | Описание |
| tтабл > tфакт, то H0 отклоняется, то есть a и b не случайно отличаются от нуля и сформировались под воздействием систематически действующего фактора x, иначе — природа формирования случайна. | |||
| Доверительные интервалы параметров линейной регрессии |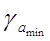 
| a- tтаблma | Если в границы доверительного интервала попадает ноль, то есть нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может принимать и положительное, и отрицательное значение. |
| a+ tтаблma | ||
| b- tтаблmb | ||
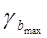
| b+ tтаблmb |
Во множественной регрессии для нахождения доверительных интервалов справедливы формулы, описанные в таблице 9:
Таблица 9
| Название характеристики | Обозначение | Формула | Описание |
| Дисперсия остатков регрессии | s2 | ESS/(n-k) | n — число единиц совокупности, k — число неизвестных параметров. |
| Дисперсия i-го коэффициента регрессии | 
| 
| 
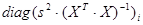
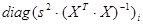— i-й элемент диагонали ковариационной матрицы
|
Продолжение таблицы 9
| Название характеристики | Обозначение | Формула | Описание |
| Доверительный интервал i-го параметра множественной регрессии |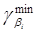 
| 
| Свойства аналогичны свойствам доверительных интервалов для парной регрессии. Табличное |
| 
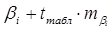
| значение t-критерия Стьюдента выбирается для n-k степеней свободы. |
