Модель качественного прогноза

Прогноз класса токсичности осуществляется на основе моделей и алгоритмов распознавания образов и теории статистических решений. Мы рассматривали задачу распознавания образов применительно к случаю двух классов. Это весьма распространенный случай, так как при любом другом числе классов последовательным разбиением на два класса можно построить разделение и на произвольное число k классов. Для этого достаточно провести k разбиений по принципу: отделить элементы первого класса от смеси остальных, затем элементы второго класса от остальных и т. д.

Обозначим через 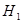соответствующий класс токсичности. Будем рассматривать объекты обучающей выборки, входящие в 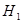, как положительные примеры класса , а объекты, не входящие в 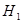, — как контрпримеры или отрицательные объекты класса , множество которых мы обозначим через . Запишем бинарный вектор наблюдений X в виде , где 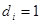 или 0 в зависимости от того, присутствует или отсутствует i-й фрагмент структуры в описании соединения. Обозначим через  и  вероятности появления i-го дескриптора в классах 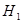 и  соответственно.

В предположении условной независимости можно записать условные плотности распределения вероятностей в каждом классе в виде произведения вероятностей для компонент вектора наблюдений.

Отношение правдоподобия при этом определяется выражением

.

Прологарифмировав это отношения и приведя подобные члены, получим байесовскую решающую функцию

 _,

где  — информационный вес k-го дескриптора, а

 — константа.

Байесовское решающее правило, минимизирующее среднюю вероятность ошибки, согласно [5], записывается следующим образом:

если  , то  , иначе .

При выводе решающего правила мы исходили из того, что потери при правильной классификации равны нулю, а при ошибочной единице. При построении систем распознавания возможны такие ситуации, когда априорные вероятности появления объектов соответствующих классов  и  неизвестны. Применительно к этой ситуации рационально использовать минимаксный критерий, который минимизирует максимально возможное значение среднего риска. Показано [16], что минимаксное правило представляет собой специальное правило Байеса для наименее благоприятных априорных вероятностей. В этом случае решающая граница выбирается так, чтобы обеспечить равенство ошибок первого и второго рода, которые соответственно равны:

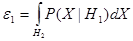 и .

Оценка величин p_i и q_i осуществляется по конечному числу выборочных представителей образов в соответствующих классах:

 ,  ,

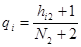где  — числа встречаемости i-го дескриптора в первом и втором классах, а 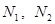 — объемы выборок в этих классах.

Отнесение химического соединения к соответствующему классу токсичности производилось в дипломном проекте по значениям  , где  — ошибка второго рода для k-го класса в зависимости от отношения правдоподобия l, а значение k, на котором достигается  , и является номером класса опасности.