Прием переструктурирования задачи

Переструктурирование заключается в изменении расположения уже имеющихся элементов задачи путем их перестановки или перегруппировки.

Задача 3

 

Акробат и собачонка

Весят два пустых бочонка.

Шустрый пес без акробата

Весит два мотка шпагата.

А с одним мотком ягненок

Весит, видите, бочонок.

Сколько весит акробат

В пересчете на ягнят?

 

Решение: Изобразим условие задачи наглядно (рис. 1), обозначив акробата буквой А, собачонка буквой С, ягненка буквой Я, бочонки буквой Б и мотки буквой М.

 

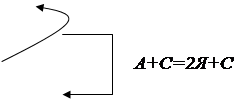А+С=Б+Б

С=М+М

Я+М=Б                                                                                 (1)

А+С=Я+М+Я+М

 

Элементы из третьего равенства переставим в первое условие, заменив каждый бочонок ягненком с мотком шпагата (2).

В равенство (2) подставим элементы второго условия, т.е. заменим два мотка шпагата собачонкой (3).

 

А+С = Я + М + Я+М (2)  А+С = 2Я + С                            (3)

 

Итак, А =2Я, акробат весит столько же, сколько и два ягненка.

Прием разбиения задачи на части

Если в задаче можно выделить самостоятельные части, то целесообразно сформулировать их отдельно и решить по очереди.

Задача 4. Заспорили три мудреца о том, кто из них самый мудрый. Наконец, они обратились к судье, славившемуся своей мудростью. «Скажи нам, справедливейший из судей, кто из нас самый мудрый?»

Задумался судья, а потом и говорит: «Вот перед вами лежат 5 тюбетеек: 3 из красного бархата, а 2 - из черного. Сейчас вам завяжут глаза и наденут тюбетейки на головы. Когда повязки с ваших глаз снимут, самый мудрый из вас скажет, какая тюбетейка у него на голове»,

Так и сделали. Сняли повязки с глаз: видит каждый перед собой красные тюбетейки на головах товарищей, а какая на своей голове — не знает. Наконец, один мудрец сказан: «О справедливейший из судей! Ты велел надеть на меня красную тюбетейку».

«Вот ты и есть самый мудрый из вас троих» - решил судья.

Как мудрец догадался, что на нем красная тюбетейка?

Решение: Так как всего было 5 тюбетеек:

3  красные и 2 черные, то возможны три различных варианта:

а) на трех мудрецов надели 2 черные и 1 красную тюбетейку;

б) на трех мудрецов надели 1 черную и 2 красные тюбетейки;

в) на трех мудрецов надели 3 красные тюбетейки.

Каждый случай можно рассмотреть отдельно.

Причем любая предыдущая подзадача помогает разобраться в последующей подзадаче.

В случае а) кто-то из мудрецов увидел бы или 2 черные тюбетейки (если на нем самом была красная), или 1 черную (если на нем была черная). А это противоречит условию, где сказано, что каждый увидел только красные тюбетейки.

В случае б) любой из собратьев обладателя черной тюбетейки увидел бы ее. А это тоже противоречит условию.

Остается случай в). К нему можно прийти без всяких дополнительных рассуждений.

Но тот, кто догадался о цвете своей тюбетейки, не знал, что каждый из спорщиков увидел только красные тюбетейки. Он мог предполагать, что на нем — черная. Но ему подсказало верный ответ молчание товарищей. Если бы кто-то из них увидел два черных головных убора, то сразу бы дал верный ответ относительно себя. Но молчание обоих свидетельствовало о том, что любой из них сомневался относительно того, какая тюбетейка у него на голове. А это могло быть только тогда, когда каждый увидел две красные тюбетейки.

Приемы моделирования

Моделью некоторого объекта А называется объект В, в каком-то отношении подобный оригиналу А, но не совпадающий с ним. Все обучение математике связано с изучением различных математических моделей: число, функция, уравнение, геометрические фигуры и т.д. Однако, работая с моделями, изучая их, учащиеся не осознают свою деятельность в этом аспекте. А школьники должны научиться изучать какие-то явления с помощью моделирования. Это существенно изменит отношение школьников к учебным занятиям.

Можно обучать приемам моделирования на таких доступных школьникам примерах, как таблицы, схемы, графы и т.п. Эти примеры имеют, быть может, не столько математическое, сколько общеинтеллектуальное значение. Рассмотрим различные приемы моделирования на конкретных задачах.

1 Прием моделирования на полупрямой

Если в задаче имеется множество объектов и требуется установить взаимоотношение между элементами этого множества, то задачу можно решать на полупрямой.

Задача 5. На вечеринку собрались четверо друзей: Аня. Вика. Миша и Коля. Коля пришел раньше Ани, но не был первым. Определите, в какой последовательности друзья приходили к месту встречи, если Вика пришла последней.

Решение: Построим модель описанной ситуации, считая обычный луч «линией времени». Друзья, пришедшие на вечеринку, обозначатся точками с соответствующими буквами. Условимся пришедшего на вечеринку раньше обозначать на полупрямой (первой буквой его имени) левее, пришедшего позже — правее. По порядку каждое условие отмечаем на полупрямой.

 

 

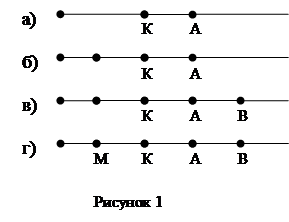
На рисунке 1, а) показано, что Коля пришел раньше Ани. По рисунку 1, б) мы видим, что кто-то из друзей опередил Колю, а следовательно, и Аню. Появление еще одной правой точки на рисунке 1, в) передает условие «Вика была последней». Тогда придется сделать вывод, что Миша пришел раньше всех. Последовательность явки друзей к месту встречи видна на рисунке 1, г).

 

2 Прием моделирования с помощью таблицы

Если в процессе решения необходимо установить соответствие между элементами двух или нескольких различных множеств, то целесообразно использовать таблицу. Поле таблицы представляет собой декартово произведение этих множеств. Количество входов в таблицу определяется количеством выделенных в задаче множеств.

Задача 6. В одном из московских вузов на разных курсах учатся четыре студента. Определить фамилию, имя, курс, на котором учится каждый студент, если известно следующее.

Борис прошлую летнюю сессию сдал на отлично;

Виктор должен был летом ехать на практику в Омск;

Иванов собирался поехать домой в Челябинск;

Антон был курсом старше Петра:

Борис и Орлов коренные москвичи:

Крылов в прошлом учебном году окончил школу и поступил на тот же факультет, на котором учился Зуев;

Борис иногда пользовался прошлогодними конспектами Виктора.

Решение: Построение модели начнем с выделения трех множеств: множество имен студентов, множество их фамилий и множество курсов. Таблица 2 с четырьмя входами охватывает все возможные соотношения между именем и фамилией, между именем и курсом и между курсом и фамилией.

Если теперь, в соответствии с условием, в таблицы 2 ставить знаки «минус» на заведомо невозможных парах элементов, то можно прийти к решению задачи.

Отметим в таблице данные из условия задачи.

Борис прошлую сессию сдал на отлично, следовательно, Борис не на I курсе — в клеточке (Борис; I) ставим знак «минус».

Виктор летом едет в Омск, а Иванов в Челябинск, значит, фамилия Виктора не Иванов — в клеточке (Виктор; Иванов) прочерк.

Антон курсом старше Петра, значит, Антон учится не на I курсе — в клеточке (Антон; I) появляется знак «минус».

Так как Борис и Орлов коренные москвичи, то фамилия Бориса не Орлов — в клеточке (Борис; Орлов) ставим прочерк.

 

Таблица 2

Имя, курс	Фамилия				Курс
	Зуев	Крылов	Иванов	Орлов	I	II	III	IV
Борис	+	-	-	-	-	-	+	+
Виктор	-	-	-	+	-	-	-	+
Антон	-	-	+	-	-	+	-	-
Петр	-	+	-	-	+	-	-	-
I	-	+	-	-
II	-	-	+	-
III	+	-	-	-
IV	-	-	-	+

 

Крылов в прошлом году окончил школу, т.е. сейчас он учится на I курсе — знак «+» в клеточке (Крылов; I). Ясно, что тогда ни Зуев, ни Иванов, ни Орлов не учатся на I курсе — в этих клеточках ставим прочерки.

Борис пользуется прошлогодними конспектами Виктора, значит, Виктор на один курс старше Бориса. Но мы знаем, что Борис уже не на I курсе, следовательно, Виктор учится не на I и не на II курсе - в клеточках (Виктор; I) и (Виктор; II) ставим прочерки.

По условию Иванов из Челябинска, а Борис коренной москвич, следовательно, Борис не Иванов - в клеточке (Борис; Иванов) прочерк.

Из таблицы видно, что на I курсе учится не Борис, не Виктор, не Антон. Следовательно, на I курсе учится Петр - в клеточке (Петр; I) появляется знак «+». В клеточках (Петр; II), (Петр; III) и (Петр; IV) прочерки.

Но на I курсе учится Крылов. Значит, Петр носит фамилию Крылов — в клеточке (Петр; Крылов) ставим знак «+». Ясно, что Петр не может быть ни Ивановым, ни Зуевым, ни Орловым, а также Крыловым не могут быть ни Борис, ни Виктор, ни Антон - во всех этих клеточках прочерки.

Обратим внимание на столбец «Иванов». Из него видно, что ни Борис, ни Виктор, ни Петр не носят фамилию Иванов. Следовательно, Ивановым может быть только Антон - в соответствующей клеточке ставим знак «+». Тогда ясно, что ни Орлов, ни Зуев не носят имя Антон - в этих клеточках появляются знаки «минус».

Обратим внимание на столбец «Орлов»: ни Борис, ни Антон, ни Петр не носят фамилию Орлов. Значит, только Виктор может быть Орловым — клеточку (Виктор; Орлов) помечаем знаком «+». Но тогда Виктор не может быть Зуевым — ставим минус в клетке (Виктор; Зуев). Тогда из таблицы видно, что только Борис может быть Зуевым.

Итак, Петр Крылов учится на I курсе, но Антон Иванов курсом старше Петра, значит, Антон Иванов на II курсе — отметим соответствующие клеточки.

Мы знаем, что Виктор Орлов курсом старше Бориса Зуева, значит, Борис Зуев учится на III, a Виктор Орлов - на IV курсе.

Задача решена. Ответ наглядно представлен в таблице.

3 Прием моделирования с помощью графов

Ситуации, в которых требуется найти соответствие между элементами различных множеств, можно моделировать с помощью графов. В этом случае элементы различных множеств будем обозначать точками, а соответствия между ними - отрезками. Пунктирные линии будут обозначать указанное в задаче отсутствие соотношения.

Задача 7. Три товарища — Иван, Дмитрий и Степан преподают различные предметы (химию, биологию и физику) в школах Москвы, Тулы и Новгорода. О них известно следующее:

1) Иван работает не в Москве, а Дмитрий - не в Новгороде;

2) москвич преподает физику;

3) тот, кто работает в Новгороде, преподает химию;

4) Дмитрий и Степан преподают не биологию;

Какой предмет, и в каком городе преподает каждый?

Решение: В задаче можно выделить три множества: учебных предметов, городов, учителей. Каждое множество содержит по три элемента. Обозначим их точками — вершинами графа (рисунок 2)

 

 

В зависимости от условий задачи будем соединять точки отрезками, если имеет место соответствие между данными элементами, или пунктирной линией, если соответствия нет.

Задача сводится к нахождению на графе трех сплошных треугольников с вершинами в разных множествах (на доске и в тетради их можно выделить разными цветами).

Так, используя условие 1), проведем пунктирную линию, соединяющую объекты Иван и Москва, Дмитрий и Новгород.

В соответствии с условием 2) соединим сплошной линией вершины Москва и физика, а условие 3) выразим сплошной линией от точки Новгород до точки химия.

Дмитрий и Степан преподают не биологию, соединим соответствующие вершины пунктирными линиями. Кто же преподает биологию? Если это не Дмитрий и не Степан, то получается, что биологию преподает Иван. Эти объекты соединяет сплошная линия.

Где же живет преподаватель биологии? Известно, что химик живет в Новгороде, а физик в Москве, следовательно, биолог живет в Туле. Обратим внимание на треугольник, образованный вершинами Иван, Тула, биология: в нем есть две сплошные стороны, значит, третью сторону также можно выделить сплошной линией. В самом деле, если Иван преподает биологию, а биолог живет в Туле, то Иван живет в Туле.

Что известно про Дмитрия? Дмитрий не живет в Новгороде (по условию) и не живет в Туле (там живет Иван), значит, Дмитрий живет в Москве - проведем соответствующую сплошную линию. Но москвич преподает физику — эта линия тоже сплошная. В треугольнике с вершинами в точках Дмитрий, Москва и физика две стороны сплошные, следовательно, третью сторону тоже можно выделить сплошной линией.

Что же известно про Степана? Степан не живет в Туле (там живет Иван) и не живет в Москве (там живет Дмитрий), следовательно, Степан живет в Новгороде - проведем сплошную линию. Но тот, кто живет в Новгороде, преподает химию — эта линия тоже сплошная. Так появляется третий треугольник из сплошных линий.

Ответ указан на графе треугольниками.

4 Приемы моделирования с помощью блок-схемы

Анализируемые ситуации полезно делать максимально наглядными. Мы уже показали различные способы наглядности (таблица, граф). Займемся теперь еще одним способом — составлением блок-схемы, где каждый шаг в рассуждении выделен отдельным изображением (прямоугольником).

Задача 8. На некотором острове отдельными селениями живут правдолюбы и шутники. Правдолюбы всегда говорят только правду, а шутники постоянно шутят, а поэтому всегда лгут. Жители одного племени бывают в селении другого, и наоборот. В одно из селений попал путешественник, но не знает, в какое именно. Доказать, что путешественнику достаточно первому встречному задать вопрос: «Вы местный?», чтобы по ответу определить, в селении какого племени он находится.

Решение: Путешественник может попасть или в селение «правдолюбов», или в селение «шутников» - появляются два различных варианта. В селении «правдолюбов» путешественник может встретить как «правдолюба», так и «шутника». Аналогично, в селении «шутников» путешественник может встретить как «шутника», так и «правдолюба». Возможных вариантов стало уже четыре (рисунок 3).

 

 

Блок-схема позволяет их представить наглядно и заметить, что положительный ответ в любом случае возможен только в селении «правдолюбов», а ответ «нет» — только в селении «шутников».