2020-01-14
334
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.
Примеры элементарных конъюнкций
.
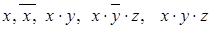Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ) и выглядит следующим образом:
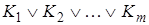
где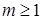 
и 
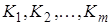- различные элементарные конъюнкций.
Примеры ДНФ:
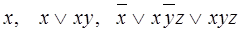
Алгоритм приведения к ДНФ может быть описан с привлечением приведенных выше равносильностей:
1. Используя закон двойного отрицания и законы Де Моргана все отрицания "спускаются" до переменных;
2. Раскрываются скобки по распределительному закону;
3. С помощью законов поглощения, противоречия и исключенного третьего удаляются лишние конъюнкции и повторение переменных;
4. С помощью соотношений с участием логическими константами, удаляются оставшиеся константы.
Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.
|
|
|
Примеры элементарных дизъюнкций:
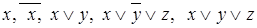
Всякая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ) и выглядит следующим образом:
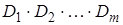
где 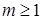и 
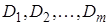- различные элементарные дизъюнкции.
Примеры КНФ:
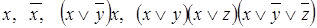
Алгоритм приведения к КНФ может быть описан с помощью тех же соотношений и законов, которые использовались и в алгоритме для ДНФ.
1. Используя закон двойного отрицания и законы Де Моргана все отрицания "спускаются" до переменных;
2. Раскрываются скобки по распределительному закону;
3. С помощью законов поглощения, противоречия и исключенного третьего удаляются лишние дизъюнкции и повторения переменных;
4. С помощью соотношений с участием логическими константами, удаляются оставшиеся константы.
Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ДНФ, в которой: 1) все слагаемые содержат сомножителем все переменные - без отрицания либо с отрицанием, но не вместе. 2) отсутствуют повторения слагаемых и сомножителей.
Совершенной конъюнктивной нормальной формой формулы алгебры высказываний (СКНФ) называется КНФ, в которой: 1) каждый сомножитель содержит слагаемым каждую переменную, без отрицания либо с отрицанием, но не вместе; 2) отсутствуют повторения сомножителей и слагаемых.
Замечание: Обратим внимание, что одно определение получается из другого заменой друг другом слов «слагаемое» и «сомножитель».
Примеры
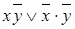— СДНФ некоторой формулы двух переменных
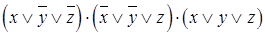- СКНФ функции трех переменных
Допустимыми для СДНФ (СКНФ) являются только некоторые полные конъюнкции (дизъюнкции): содержащие — без повторений — все переменные этой функции — с отрицаниями или без них.
|
|
|
Опишем два способа приведения к совершенным нормальным формам.
1-Й СПОСОБ — АНАЛИТИЧЕСКИЙ
Алгоритм приведение к СДНФ:
1.Приводят к ДНФ с помощью равносильных преобразований;
2. Умножают на единицы, представленные в виде дизъюнкций каждой недостающей переменной, с ее отрицанием;
3.Раскрывают скобки — по первому распределительному закону;
4.Исключают повторения слагаемых.
Пример:
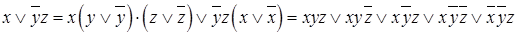
Алгоритм приведение к СКНФ:
1. Формулу приводят к КНФ;
2. Прибавляют нули, представленные в виде конъюнкций каждой недостающей переменной с ее отрицанием;
3. С помощью второго распределительного закона приводят эти сомножители к суммам первой степени, т. е. не содержащим произведений;
4. Исключают повторения сомножителей.
Пример:
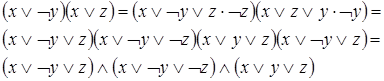
2-Й СПОСОБ — ТАБЛИЧНЫЙ
Составим таблицу истинности для функции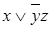 
:
| x | y | z |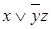 
|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Алгоритм приведение к СДНФ:
1. Строим таблицу истинности;
2. Рассматриваем только те строки таблицы, в которых формула принимает значение 1;
3. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 — без отрицания;
4. Образуем дизъюнкцию всех полученных конъюнкций.
Пример: В нашей таблице первую строку опускаем: функция принимает значение 0. Второй строке соответствует конъюнкция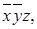 
третью строку опускаем и т. д.
СДНФ:
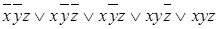
Приведение к СКНФ:
1.Строим таблицу истинности;
2.Рассматриваем только те строки таблицы, где функция принимает значение 0;
3.Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Аргумент, принимающий значение 0, берется без отрицания, значение 1 — с отрицанием;
4.Образуют конъюнкцию полученных дизъюнкций.
В нашем примере первой строке таблицы соответствует дизъюнкция
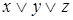
вторую строку опускаем и т. д.
СКНФ:
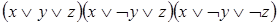
Замечания:
1) Если условиться из двух совершенных форм, СДНФ и СКНФ, отдавать предпочтение той, которая содержит меньше букв, то СДНФ предпочтительнее, если в столбце значений функции таблицы истинности меньше единиц; СКНФ — если в этом столбце меньше нулей.
2) В обычной, школьной алгебре мы знаем, что нет общего метода перехода от табличного задания функции к аналитическому. В алгебре высказываний, как видим, такой метод существует /5,7/.
