Под термином ``алгебра'' в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие  . Используются определения и обозначения из работы [1]. Дополнительно отметим, что конгруэнции произвольной алгебры обозначаются греческими буквами. Если
. Используются определения и обозначения из работы [1]. Дополнительно отметим, что конгруэнции произвольной алгебры обозначаются греческими буквами. Если  - конгруэнция на алгебре
- конгруэнция на алгебре  , то
, то  - класс эквивалентности алгебры
- класс эквивалентности алгебры  по конгруэнции
по конгруэнции  ,
, 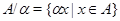 - факторалгебра алгебры
- факторалгебра алгебры  по конгруэнции
по конгруэнции  . Если
. Если  и
и  - конгруэнции на алгебре
- конгруэнции на алгебре  ,
,  , то конгруэнцию
, то конгруэнцию  на алгебре
на алгебре  назовем фактором на
назовем фактором на  . Очевидно, что
. Очевидно, что  тогда и только тогда, когда
тогда и только тогда, когда  .
. 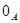 или
или  и
и  или
или  - соответственно наименьший и наибольший элементы решетки конгруэнций алгебры
- соответственно наименьший и наибольший элементы решетки конгруэнций алгебры  .
.
Будем пользоваться следующим определением централизуемости конгруэнций, эквивалентность которого определению Смита [5] доказана в работе [6].
Определение 2.1. Пусть  и
и  - конгруэнции на алгебре
- конгруэнции на алгебре  . Тогда
. Тогда  централизует
централизует  (записывается:
(записывается:  ), если на
), если на  существует такая конгруэнция
существует такая конгруэнция  , что:
, что:
1) из  всегда следует
всегда следует  ;
;
2) для любого элемента  всегда выполняется
всегда выполняется
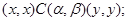
3) если  , то
, то  .
.
Следующие свойства централизуемости, полученные Смитом [5], сформулируем в виде леммы.
Лемма 2.1. Пусть  . Тогда:
. Тогда:
 существует единственная конгруэнция
существует единственная конгруэнция  , удовлетворяющая определению 2.1;
, удовлетворяющая определению 2.1;

 ;
;
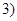 если
если  , то
, то  .
.
Из леммы 2.1 и леммы Цорна следует, что для произвольной конгруэнции  на алгебре
на алгебре  существует такая единственная наибольшая конгруэнция
существует такая единственная наибольшая конгруэнция  , что
, что  . Эту конгруэнцию
. Эту конгруэнцию  будем называть централизатором конгруэнции
будем называть централизатором конгруэнции  в
в  и обозначать
и обозначать 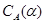 .
.
Лемма 2.2. Пусть 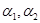 - конгруэнции на алгебре
- конгруэнции на алгебре  ,
, 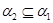 ,
,  ,
,  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:

 ;
;
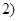
 , где
, где  ;
;
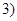 если,
если,  , либо
, либо
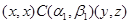 , либо
, либо
 , то всегда
, то всегда 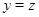 ;
;
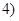 из
из  всегда следует
всегда следует  .
.
Доказательство. 1). Очевидно, что  - конгруэнция на
- конгруэнция на 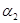 , удовлетворяющая определению 1. Значит, в силу п.1) леммы 2.1
, удовлетворяющая определению 1. Значит, в силу п.1) леммы 2.1 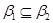 .
.
2).  - конгруэнция на
- конгруэнция на  , удовлетворяющая определению 2.1. Значит,
, удовлетворяющая определению 2.1. Значит,  .
.
3). Пусть  . Тогда
. Тогда

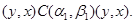
Применим к последним трем соотношениям мальцевский оператор  такой, что
такой, что  , для любых элементов
, для любых элементов  . Тогда получим
. Тогда получим

Аналогичным образом доказываются остальные случаи п.3).
4). Пусть  . Тогда справедливы следующие соотношения:
. Тогда справедливы следующие соотношения:



Следовательно,  , где
, где  - мальцевский оператор. Тогда
- мальцевский оператор. Тогда  , т.е.
, т.е.  . Так как
. Так как  и
и 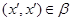 , то
, то  . Таким образом
. Таким образом  . Лемма доказана.
. Лемма доказана.
В дальнейшем мы будем часто ссылаться на следующий хорошо известный факт (доказательство см., например [6]).
Лемма 2.3. Любая подалгебра алгебры  , содержащая конгруэнцию
, содержащая конгруэнцию 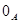 , является конгруэнцией на
, является конгруэнцией на  .
.
Доказательство следующего результата работы [5] содержит пробел (следствие 224 [5] неверно, см. [7]), поэтому докажем его.
Лемма 2.4. Пусть  . Тогда для любой конгруэнции
. Тогда для любой конгруэнции  на
на 
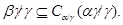
Доказательство. Обозначим  и определим на алгебре
и определим на алгебре  бинарное отношение
бинарное отношение  следующим образом:
следующим образом:

тогда и только тогда, когда 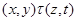 , где
, где  ,
,  . Используя лемму 2.3, нетрудно показать, что
. Используя лемму 2.3, нетрудно показать, что  - конгруэнция на алгебре
- конгруэнция на алгебре 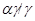 , причем
, причем  .
.
Пусть  , т.е.
, т.е.  ,
,  . Тогда
. Тогда  и, значит,
и, значит,  .
.
Пусть, наконец, имеет место  и
и  . Тогда справедливы следующие соотношения:
. Тогда справедливы следующие соотношения:



Применяя мальцевский оператор  к этим трем соотношениям, получаем:
к этим трем соотношениям, получаем:  . Из леммы 2.2 следует, что
. Из леммы 2.2 следует, что  . Так как
. Так как  и
и  , то
, то  . Значит,
. Значит, 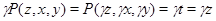 . Но
. Но  , следовательно,
, следовательно,  . Итак,
. Итак,  и удовлетворяет определению 2.1. Лемма доказана.
и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5. Пусть 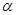 и
и  - конгруэнции на алгебре
- конгруэнции на алгебре  ,
,  и
и  - изоморфизм, определенный на
- изоморфизм, определенный на  . Тогда для любого элемента
. Тогда для любого элемента  отображение
отображение  определяет изоморфизм алгебры
определяет изоморфизм алгебры  на алгебру
на алгебру  , при котором
, при котором  . В частности,
. В частности,  .
.
Доказательство. Очевидно, что  - изоморфизм алгебры
- изоморфизм алгебры  на алгебру
на алгебру  , при котором конгруэнции
, при котором конгруэнции  ,
, 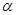 изоморфны соответственно конгруэнциям
изоморфны соответственно конгруэнциям  и
и  . Так как
. Так как  , то определена конгруэнция
, то определена конгруэнция  , удовлетворяющая определению 2.1. Изоморфизм
, удовлетворяющая определению 2.1. Изоморфизм  алгебры
алгебры 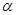 на алгебру
на алгебру  индуцирует в свою очередь изоморфизм
индуцирует в свою очередь изоморфизм  алгебры
алгебры  на алгебру
на алгебру  такой, что
такой, что 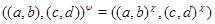 для любых элементов
для любых элементов  и
и  , принадлежащих
, принадлежащих  . Но тогда легко проверить, что
. Но тогда легко проверить, что  - конгруэнция на алгебре
- конгруэнция на алгебре  изоморфная конгруэнции
изоморфная конгруэнции  . Это и означает, что
. Это и означает, что  . Лемма доказана.
. Лемма доказана.
Если 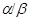 и
и 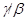 - факторы на алгебре
- факторы на алгебре  такие, что
такие, что  , то конгруэнцию
, то конгруэнцию  обозначим через
обозначим через  и назовем централизатором фактора
и назовем централизатором фактора  в
в  .
.
Напомним, что факторы 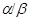 и
и  на алгебре
на алгебре  называются перспективными, если либо
называются перспективными, если либо  и
и  , либо
, либо 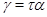 и
и 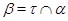 .
.
Докажем основные свойства централизаторов конгруэнций.
Теорема 2.1. Пусть  - конгруэнции на алгебре
- конгруэнции на алгебре  . Тогда:
. Тогда:
 если
если  , то
, то 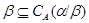 ;
;
 если
если 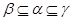 , то
, то  ;
;
 ;
;
 если
если  ,
,  и факторы
и факторы 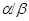 ,
, 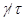 перспективны, то
перспективны, то

 если
если  - конгруэнции на
- конгруэнции на  и
и 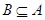 , то
, то

Доказательство. 1). Так как конгруэнция  централизует любую конгруэнцию и
централизует любую конгруэнцию и  , то
, то  .
.
2). Из п.1) леммы 2.2 следует, что  , а в силу леммы 2.4 получаем, что
, а в силу леммы 2.4 получаем, что  .
.
Пусть  - изоморфизм
- изоморфизм  . Обозначим
. Обозначим

По лемме 2.5  , а по определению
, а по определению

Следовательно, 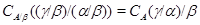 .
.
3). Очевидно, достаточно показать, что для любых двух конгруэнций  и
и  на алгебре
на алгебре  имеет место равенство:
имеет место равенство:

Покажем вначале, что

Обозначим  . Тогда, согласно определения 2.1, на алгебре
. Тогда, согласно определения 2.1, на алгебре  существует такая конгруэнция
существует такая конгруэнция 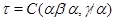 , что выполняются следующие свойства:
, что выполняются следующие свойства:
а) если  , то
, то 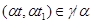 ;
;
б) для любого элемента  ,
,  ;
;
в) если 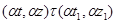 и
и  , то
, то  .
.
Построим бинарное отношение  на алгебре
на алгебре  следующим образом:
следующим образом:

тогда и только тогда, когда  и
и  ,
,  . Покажем, что
. Покажем, что  - конгруэнция на
- конгруэнция на  . Пусть
. Пусть  ,
,  . Тогда
. Тогда  и
и 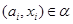 ,
,  . Так как
. Так как  - конгруэнция, то для любой
- конгруэнция, то для любой  -арной операции
-арной операции  имеем:
имеем:

Очевидно, что ( ,
, 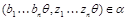 и
и 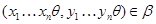 ,
,  . Следовательно,
. Следовательно, 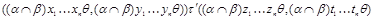 . Очевидно, что для любой пары
. Очевидно, что для любой пары  . Значит,
. Значит,  . Итак, по лемме 2.3,
. Итак, по лемме 2.3,  - конгруэнция на
- конгруэнция на  . Покажем теперь, что
. Покажем теперь, что  удовлетворяет определению 2.1, т.е.
удовлетворяет определению 2.1, т.е.  централизует
централизует  .
.
Пусть
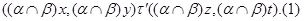
Тогда  и
и  . Так как
. Так как  ,
,  и
и 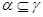 , то
, то  . Следовательно,
. Следовательно,  удовлетворяет определению 2.1.
удовлетворяет определению 2.1.
Если  , то
, то  , значит,
, значит,

Пусть, наконец, имеет место (1) и

Тогда  . Так как
. Так как  и
и  , то
, то  , следовательно,
, следовательно,  . Из (2) следует, что
. Из (2) следует, что  , а по условию
, а по условию  . Значит,
. Значит,  и поэтому
и поэтому  . Тем самым показано, что конгруэнция
. Тем самым показано, что конгруэнция  удовлетворяет определению 2.1, т.е.
удовлетворяет определению 2.1, т.е. 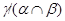 централизует
централизует  . Докажем обратное включение. Пусть
. Докажем обратное включение. Пусть  . Тогда на алгебре
. Тогда на алгебре  определена конгруэнция
определена конгруэнция 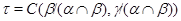 , удовлетворяющая определению 2.1. Построим бинарное отношение
, удовлетворяющая определению 2.1. Построим бинарное отношение  на алгебре
на алгебре  следующим образом:
следующим образом:
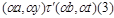
тогда и только тогда, когда

и  ,
,  . Аналогично, как и выше, нетрудно показать, что
. Аналогично, как и выше, нетрудно показать, что  - конгруэнция на алгебре
- конгруэнция на алгебре  . Заметим, что из доказанного включения
. Заметим, что из доказанного включения  следует, что
следует, что 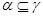 . Покажем поэтому, что
. Покажем поэтому, что  централизует
централизует  . Так как
. Так как  ,
, 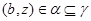 и
и  , то
, то  , т.е.
, т.е.  удовлетворяет условию 1) определения 2.1.
удовлетворяет условию 1) определения 2.1.
Если  , то
, то  , следовательно,
, следовательно,  .
.
Пусть имеет место (3) и  . Так как
. Так как  ,
,  , то
, то  и
и  . Из (4) следует, что
. Из (4) следует, что  , следовательно,
, следовательно,  , т.е.
, т.е.  . На основании леммы 2.2 заключаем, что
. На основании леммы 2.2 заключаем, что  . Следовательно,
. Следовательно,  . Но так как
. Но так как  , то
, то 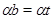 , т.е.
, т.е.  .
.
4) Обозначим  . Пусть
. Пусть  и удовлетворяет определению 2.1. Определим бинарное отношение
и удовлетворяет определению 2.1. Определим бинарное отношение  на
на  следующим образом
следующим образом  тогда и только тогда, когда
тогда и только тогда, когда  . Аналогично, как и выше, нетрудно показать, что
. Аналогично, как и выше, нетрудно показать, что  - конгруэнция, удовлетворяющая определению 2.1. Это и означает, что
- конгруэнция, удовлетворяющая определению 2.1. Это и означает, что 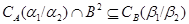 . Теорема доказана.
. Теорема доказана.
Как следствие, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.
Мультикольцо
Согласно [2] алгебра  сигнатуры
сигнатуры  называется мультикольцом,если алгебра
называется мультикольцом,если алгебра  -группа(не обязательно абелева).Все операции из
-группа(не обязательно абелева).Все операции из  имеют ненулевые арности и для любой
имеют ненулевые арности и для любой  -арной операции
-арной операции  и любых элементов
и любых элементов 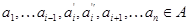 имеет место
имеет место  =
=  ,для любого
,для любого  . Заметим,что мультикольцо является дистрибутивной
. Заметим,что мультикольцо является дистрибутивной  -группой в смысле определения Хиггинса [10] или мультиоператорной группой согласно А.Г.Куроша [9]. Для мультиколец справедливы следующие равенства:
-группой в смысле определения Хиггинса [10] или мультиоператорной группой согласно А.Г.Куроша [9]. Для мультиколец справедливы следующие равенства:


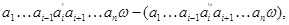
где 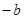 ,как обычно, обозначается элемент,противоположный к элементу
,как обычно, обозначается элемент,противоположный к элементу  .
.
Докажем,например,первое равенство.
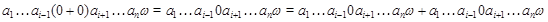
Прибавляя к обеим частям равенства элемент,противоположный к элементу

получаем требуемое равенство.
Определение. Подалгебра  мультикольца
мультикольца  называется идеалом [9],если
называется идеалом [9],если  -нормальная подгруппа группы
-нормальная подгруппа группы  и для любой
и для любой  -арной операции
-арной операции  , произвольного
, произвольного  и любых
и любых  ,
,  имеет место
имеет место

В частности,если  -нульарная или унарная операция,то это означает,что
-нульарная или унарная операция,то это означает,что
Как следует из примера [8] конгруэнции на мультикольце перестановочны. Следующая теорема устанавливает соответствие между идеалами и конгруэнциями мультикольца.
Теорема 3.1 [2] Пусть 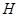 -идеал мультикольца
-идеал мультикольца  и
и

Тогда  -конгуэнция на
-конгуэнция на  и любая конгруэнция на
и любая конгруэнция на  имеет такой вид для подходящего идеала
имеет такой вид для подходящего идеала 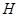 .
.
Доказательство.
Так как

то  . Покажем,что
. Покажем,что  -подалгебра алгебры
-подалгебра алгебры  .Проверим вначале замкнутость
.Проверим вначале замкнутость  относительно групповых операций. Пусть
относительно групповых операций. Пусть  , т.е.
, т.е.  . Тогда в силу того,что
. Тогда в силу того,что  ,получаем
,получаем

т.е. 

т.е. 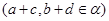 . Пусть теперь
. Пусть теперь 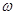 -n-арная операция и
-n-арная операция и  ,
,  Так как
Так как 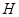 -идеал,то получаем
-идеал,то получаем

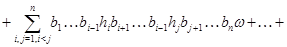
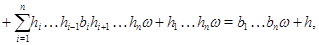
т.е.  . Теперь из леммы [8] следует,что
. Теперь из леммы [8] следует,что  -конгруэнция на
-конгруэнция на  . Обратно,пусть
. Обратно,пусть  -конгруэнция на
-конгруэнция на  . Положим
. Положим

Из [8] следует,что 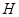 -нормальная подгруппа группы
-нормальная подгруппа группы  . Аналогичным образом,как и в [8],показывается,что
. Аналогичным образом,как и в [8],показывается,что 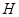 -идеал мультикольца
-идеал мультикольца  . Теорема доказана.
. Теорема доказана.
Следствие 3.2. Решетка идеалов мультикольца  изоморфна решетке его конгруэнций.
изоморфна решетке его конгруэнций.
Определение 3.3 [3].Пусть 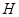 -идеал мультикольца
-идеал мультикольца  .Тогда централизатором
.Тогда централизатором 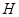 в
в  называется наибольший идеал
называется наибольший идеал  в
в  такой,что для любого
такой,что для любого  и любого
и любого  выполняются следующие условия:
выполняются следующие условия:
1)  ;
;
2) для любой  -арной операции
-арной операции 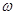
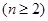 ,любых различных
,любых различных  ,произвольных
,произвольных  справедливо
справедливо

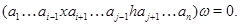
Теорема 3.4. Пусть  и
и  -идеалы мультикольца
-идеалы мультикольца  и
и 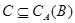 . Тогда
. Тогда  и
и 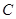 индуцируют на
индуцируют на  соответственно конгруэнции
соответственно конгруэнции 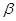 и
и  , где
, где

тогда

Доказательство:
Определим бинарное отношение  на
на  следующим образом
следующим образом  тогда и только тогда, когда найдутся такие элементы
тогда и только тогда, когда найдутся такие элементы  и
и  ,что справедливы равенства
,что справедливы равенства

Очевидно,что  -отношенме эквивалентности на
-отношенме эквивалентности на  , удовлетворяющее условиям 1)-3) определения 2.1.,замкнутость которого относительно групповых операций доказана в примере [8]
, удовлетворяющее условиям 1)-3) определения 2.1.,замкнутость которого относительно групповых операций доказана в примере [8]
Пусть теперь 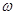 -
-  -арная операция и
-арная операция и  Тогда
Тогда
 и
и 
для любых  Следовательно,
Следовательно,

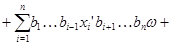


Подставляя в правую часть последнего равенства значения 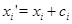 и учитывая,что после раскрытия скобок члены,одновременно содержащие элементы
и учитывая,что после раскрытия скобок члены,одновременно содержащие элементы  и
и 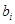 ,равны нулю
,равны нулю  , получаем в правой части равенства выражение
, получаем в правой части равенства выражение



Так как  -идеал,то
-идеал,то



Итак,

тогда  .
.
Теорема 3.5 Пусть  и
и  -идеалы мультикольца
-идеалы мультикольца  ,
,  ,
,  -конгруэнции,определенные в теореме 3.4. и
-конгруэнции,определенные в теореме 3.4. и  .Тогда
.Тогда  .
.
Доказательство: Пусть  -конгруэнции мультикольца
-конгруэнции мультикольца  и
и  . Обозначим смежные классы по
. Обозначим смежные классы по  и
и 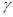 ,являющиеся идеалами мультикольца, соответственно
,являющиеся идеалами мультикольца, соответственно 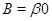 и
и 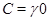 . Возьмем произвольные элементы
. Возьмем произвольные элементы  ,
,  ,
,  . Тогда
. Тогда


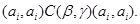
Следовательно,для любой  -арной операции
-арной операции  , любых различных
, любых различных  получаем
получаем
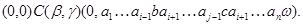
Из определения 2.1. следует,что
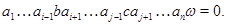
Очевидно,что справедливо и другое аналогичное равенство определения [8] Т.к. из примера [8] следует,что  ,то это означает, что
,то это означает, что  .
.
Очевидно,что из теорем 3.4. и 3.5. и результатов раздела 2 следуют все известные свойства централизаторов подгрупп,а так же свойства централизаторов идеалов мультиколец работы [3](Лемма 2.8).
ЗАКЛЮЧЕНИЕ
В настоящей дипломной работе решается задача взаимосвязи структуры мультиколец и универсальных алгебр, получен новый результат: идеал  тогда и только тогда централизуется идеалом
тогда и только тогда централизуется идеалом  , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
, когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
Результаты данной дипломной работы могут быть использованы при чтении спецкурса для студентов математического факультета,а так же аспирантами и научными сотрудниками,занимающимися проблемами современной алгебры.
 2020-01-14
2020-01-14 77
77








