Преобразования Лоренца. Следствия из СТО

Рассмотрим две ИСО . Пусть система движется относительно со скоростью 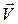. В начальный момент времени , из начала координат, когда совпадают, излучается световой сигнал. За время в системе сигнал дойдет до точки А,пройдя расстояние , в системе координата светового импульса будет , где 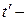время прохождения светового импульса от начала координат до точки А в системе .

Связь между координатами точки А в системах , и , которая движется относительно со скоростью вдоль положительного направления оси , осуществляется с помощью преобразований Лоренца (без вывода):

(7.1)

где координаты и время сигнала относительно системы ;

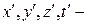координаты и время сигнала относительно системы .

Преобразования Лоренца симметричны и сохраняют свой вид при переходе от системы к системе с переменой знака у :

, (7.2)

Следствия из СТО.

1. Для обычного трехмерного пространства (евклидового)

, (7.3)

где 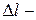расстояние между двумя точками.

В четырехмерном пространстве интервал между событиями с координатами: и с координатами находится по формуле:

(7.4)

Пространство, для которого 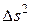определяется формулой (7.4) называется псевдоевклидовым.

Из (7.4) следует, что

, (7.5)

где .

Следовательно, четырехмерное пространство – псевдоевклидово.

2. Линейный размер тела, движущегося вместе с относительно , уменьшается в направлении движения. Это изменение продольного размера тела (по направлению относительного движения) называется лоренцевым сокращением длины и фиксируется в условно неподвижной системе .

Длина тела относительно неподвижной системы отсчета

, (7.6)

где собственная длина (длина тела, измеренная в системе, относительно которой тело покоится (система )); длина тела, измеренная в системе, относительно которой тело движется (система ).

В СТО линейные размеры тела относительны, хотя поперечные размеры тела не зависят от скорости его движения.

Лоренцево сокращение длины тела является кинематическим релятивистским эффектом. Оно не связано с действием на движущееся тело каких-либо продольных сил, сжимающих его вдоль направления движения, и обусловлено определенной процедурой измерения размеров движущегося тела. Это сокращение существенно только при .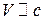

3. Пусть тело покоится относительно движущейся системы и движется относительно неподвижной системы (движется вместе с системой ). Время, отсчитанное по часам, движущимся вместе с телом, называется собственным временем этого тела и обозначается буквой . Время, отсчитанное по часам неподвижной системы отсчета , относительно которой тело движется со скоростью 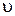, обозначается буквой .

Промежуток времени между двумя событиями, произошедшими в системе , обозначим , а промежуток времени между двумя этими же событиями в системе , обозначим . Тогда, из преобразований Лоренца можно получить

. (7.7)

Согласно (7.7) ; т.е. собственное время всегда меньше, чем время, отсчитанное по неподвижным часам, или движущиеся часы в системе идут медленнее, чем совершенно такие же, но покоящиеся часы в системе . Этот эффект называется замедлением времени (релятивистский эффект замедления хода времени). Причем наблюдатель, который движется, вместе с системой , не заметит, что его часы идут медленнее, чем часы в системе . Пример: (Два близнеца. Один улетит в космос со скоростью света, другой останется на Земле. Через 30 лет, прилетевший останется молодым, а на Земле его встретит брат старик).

4. Причинность.

Последовательность хода событий причина – следствие в релятивистской механике является неизменной, и порядок следования причинно-следственных событий одинаков во всех ИСО.

5. Релятивистский закон преобразования скоростей (без вывода).

Если частица движется относительно со скоростью , тогда

, (7.8)

где 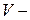скорость системы относительно ; скорость частицы относительно .

6. Возрастание массы движущегося тела с увеличением скорости движения.

Из закона сохранения импульса, используя преобразования Лоренца, можно показать, что масса движущегося со скоростью тела (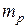) больше массы того же самого покоящегося тела (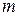), т.е.

7. При формулы релятивистской механики переходят в формулы нерелятивистской механики (принцип соответствия).

7.2. Импульс и энергия релятивистской частицы. Энергия покоя.

Релятивистский импульс частицы

, (7.9)

где масса частицы; скорость движения частицы.

Полная релятивистская энергия частицы

, (7.10)

где энергия покоя частицы (внутренняя энергия частицы, не связанная с движением частицы как целого).

Релятивистское выражение для кинетической энергии частицы

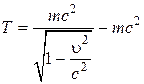. (7.11)

(7.10) с учетом (7.11) (7.12)

Связь полной энергии частицы и ее импульса

, (7.13)

7.3. Законы сохранения энергии и импульса.

Элементарные частицы движутся со скоростями .

Для замкнутой системы сталкивающихся (взаимодействующих) частиц выполняются законы сохранения (для любого взаимодействия):

1) полной релятивистской энергии

, (7.14)

формулировка: суммарная полная энергия релятивистских частиц до взаимодействия равна суммарной полной энергии релятивистских частиц после взаимодействия;

2) импульса

, (7.15)

формулировка: суммарный импульс релятивистских частиц до взаимодействия равен суммарному импульсу релятивистских частиц после взаимодействия, где

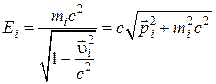
и аналогично для штрихованных величин.

Так как 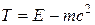, то из (7.14) получим

, (7.16)

где .

Величинa представляет собой энергию, выделяющуюся или поглощающуюся 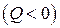в процессе столкновения. В случае ядерных реакций называют энергетическим выходом ядерной реакции.