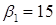2020-01-14
104
Определите максимальные стратегии игроков и седловую точку игры
| Игрок | В1 | В2 | В3 | В4 | В5 |
| А1 | 5 | 8 | 7 | 6 | 3 |
| А2 | 10 | 12 | 4 | 7 | 2 |
| А3 | 15 | 10 | 8 | 7 | 4 |
| А4 | 10 | 7 | 8 | 12 | 6 |
| А5 | 7 | 10 | 11 | 3 | 5 |
| А6 | 7 | 2 | 3 | 12 | 4 |
Решение: Строки матрицы соответствуют стратегиям Аi (i=1,2,…,m), то есть стратегиям, которые выбирает игрок А. Столбцы – стратегии Вi,то есть стратегии, которые выбирает игрок В.
· Игрок А выбирает такую стратегию, чтобы максимизировать свой минимальный выигрыш 
:
,
где а – нижняя цена игры (гарантированный выигрыш игрока А)
· Игрок В выбирает такую стратегию, при которой его максимальный проигрыш
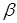- минимизируется:
,
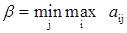где 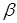- верхняя цена игры.
Составим расчетную таблицу.
коммерческий математический моделирование линейный программирование
| 1 2 | В1 | В2 | В3 | В4 | В5 | 
| |
| А1 | 5 | 8 | 7 | 6 | 3 |  3
| |
| А2 | 10 | 12 | 4 | 7 | 2 |  2
| |
| А3 | 15 | 10 | 8 | 7 | 4 |  4
| |
| А4 | 10 | 7 | 8 | 12 | 6 |  6
| |
| А5 | 7 | 10 | 11 | 3 | 5 |  3
| |
| А6 | 7 | 2 | 3 | 12 | 4 |  2
| |
|
|  12
|  11
|  12
|  6
|  6
 6
| |
Этот выигрыш 
гарантирован игроку 1, как бы ни играл второй игрок.
Нижняя цена игры составляет 6
Минимальный проигрыш второго игрока 
Получили, что первый игрок (А) должен выбрать пятую (А4) стратегию, а второй игрок (В) должен выбрать четвертую (В5) стратегию.
Итак, нижняя цена игры, или максимальный выигрыш: , верхняя цена игры, или минимальный выигрыш:
Нижняя и верхняя цена игры равны и достигаются на одной и той же паре стратегий
(А4;В5). Следовательно, игра имеет седловую точку (А4;В5).
Вывод: Игрок А должен выбрать четвертую стратегию, а игрок В пятую стратегию при этом выигрыш первого игрока будет максимальным из максимальных как бы ни играл второй игрок, а второй игрок минимально проиграет. Игра имеет седловую точку (А4;В5).
