Напомним, что класс  алгебр сигнатуры
алгебр сигнатуры  называется многообразием, если существует множество
называется многообразием, если существует множество  тождеств сигнатуры
тождеств сигнатуры  такое, что алгебра сигнатуры
такое, что алгебра сигнатуры  принадлежит классу
принадлежит классу  тогда и только тогда, когда в ней выполняются все тождества из множества
тогда и только тогда, когда в ней выполняются все тождества из множества  .
.
Многообразие называется мальцевским, если оно состоит из алгебр, в которых все конгруэнции перестановочны.
Все алгебры считаются принадлежащими некоторому фиксированному мальцевcкому многообразию. Используются стандартные обозначения и определения из[2].
В данной работе конгруэнции произвольной алгебры будем обозначать греческими буквами.
Если  – конгруэнция на алгебре
– конгруэнция на алгебре  , то
, то

смежный класс алгебры  по конгруэнции
по конгруэнции  .
. 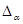 или
или  – диагональ алгебры
– диагональ алгебры 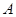 .
.
Для произвольных конгруэнции  и
и 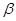 на алгебре
на алгебре 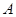 будем обозначать
будем обозначать  множество всех конгруэнции на алгебре
множество всех конгруэнции на алгебре  таких, что
таких, что

тогда и только тогда, когда

Так как  , то множество
, то множество 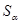 не пусто.
не пусто.
Следующее определение дается в работе[2].
Определение 2.1. Пусть  и
и 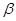 – конгруэнции на алгебре
– конгруэнции на алгебре 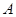 . Тогда
. Тогда  централизует
централизует  (записывается:
(записывается: 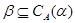 ), если на
), если на  существует такая конгруэнция
существует такая конгруэнция  , что:
, что:
1) из
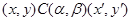
всегда следует

2) для любого элемента

всегда выполняется

3) если

то
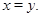
Под термином «алгебра» в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие  .
.
Следующие свойства централизуемости, полученные Смитом[3], сформулируем в виде леммы.
Лемма 2.1. Пусть 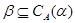 . Тогда:
. Тогда:
1) существует единственная конгруэнция  , удовлетворяющая определению 2.1;
, удовлетворяющая определению 2.1;
2)  ;
;
3) если

то
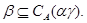
Из леммы 2.1. и леммы Цорна следует, что для произвольной конгруэнции  на алгебре
на алгебре 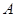 всегда существует наибольшая конгруэнция, централизующая
всегда существует наибольшая конгруэнция, централизующая  . Она называется централизатором конгруэнции
. Она называется централизатором конгруэнции  в
в 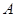 и обозначается
и обозначается  .
.
В частности, если 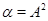 , то централизатор
, то централизатор  в
в 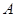 будем обозначать
будем обозначать  .
.
Лемма 2.2. Пусть 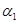 ,
, 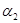 – конгруэнции на алгебре
– конгруэнции на алгебре 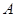 ,
, 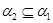 ,
,  ,
,  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1)  ;
;
2)  , где
, где 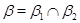 ;
;
3) если выполняется одно из следующих отношений:




4) из  всегда следует
всегда следует
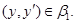
Доказательство:
1) Очевидно, что 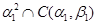 – конгруэнция на
– конгруэнция на 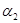 , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и
, удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и 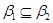 .
.
2) 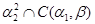 – конгруэнция на
– конгруэнция на 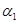 , удовлетворяющая определению 2.1. Значит
, удовлетворяющая определению 2.1. Значит

3) Пусть  . Тогда
. Тогда


Применим к последним трем соотношениям мальцевский оператор  такой, что
такой, что

Тогда получим

т.е.

Аналогичным образом показываются остальные случаи из пункта 3).
4) Пусть

Тогда справедливы следующие соотношения:

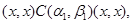

Следовательно,

где  – мальцевский оператор.
– мальцевский оператор.
Тогда
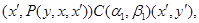
то есть  .
.
Так как

то 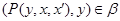 .
.
Таким образом 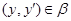 . Лемма доказана.
. Лемма доказана.
Следующий результат оказывается полезным при доказательстве последующих результатов.
Лемма. 2.3. Любая подалгебра алгебры 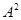 , содержащая диагональ
, содержащая диагональ  , является конгруэнцией на алгебре
, является конгруэнцией на алгебре 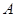 .
.
Доказательство:
Пусть
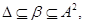
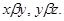
Тогда из



следует, что

Аналогичным образом из



получаем, что

Итак, 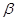 симметрично и транзитивно. Лемма доказана.
симметрично и транзитивно. Лемма доказана.
Доказательство следующего результата работы [1] содержит пробел, поэтому докажем его.
Лемма 2.4. Пусть 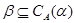 . Тогда
. Тогда  для любой конгруэнции
для любой конгруэнции  на алгебре
на алгебре 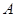 .
.
Доказательство:
Обозначим  и определим на алгебре
и определим на алгебре  бинарное отношение
бинарное отношение 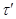 следующим образом:
следующим образом:

тогда и только тогда, когда

где


Используя лемму 2.3, нетрудно показать, что 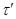 – конгруэнция на алгебре
– конгруэнция на алгебре  , причем
, причем

Пусть

то есть


Тогда

и, значит

Пусть, наконец, имеет место

Тогда справедливы следующие соотношения:
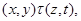
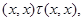

применяя мальцевчкий оператор  к этим трем соотношениям, получаем
к этим трем соотношениям, получаем

Из леммы 2.2 следует, что

Так как

то

Значит,

Но  , следовательно,
, следовательно,  .
.
Итак,
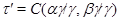
и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5. Пусть 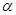 ,
, 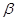 – конгруэнции на алгебре
– конгруэнции на алгебре  ,
,  и
и  – изоморфизм, определенный на
– изоморфизм, определенный на 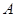 .
.
Тогда для любого элемента  отображение
отображение  определяет изоморфизм алгебры
определяет изоморфизм алгебры 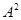 на алгебру
на алгебру  , при котором
, при котором  .
.
В частности,  .
.
Доказательство.
Очевидно, что  – изоморфизм алгебры
– изоморфизм алгебры 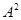 на алгебру
на алгебру  , при котором конгруэнции
, при котором конгруэнции 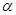 ,
, 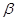 изоморфны соответственно конгруэнциям
изоморфны соответственно конгруэнциям  и
и  .
.
Так как

то определена конгруэнция

удовлетворяющая определению 2.1.
Изоморфизм  алгебры
алгебры 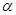 на алгебру
на алгебру  индуцирует в свою очередь изоморфизм
индуцирует в свою очередь изоморфизм  алгебры
алгебры  на алгебру
на алгебру 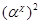 такой, что
такой, что
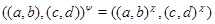
для любых элементов  и
и  , принадлежащих
, принадлежащих 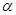 . Но тогда легко проверить, что
. Но тогда легко проверить, что  – конгруэнция на алгебре
– конгруэнция на алгебре 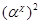 , изоморфная конгруэнции
, изоморфная конгруэнции 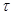 .
.
Это и означает, что

Лемма доказана.
Определение 2.2. Если  и
и  – факторы на алгебре
– факторы на алгебре  такие, что
такие, что

то конгруэнцию 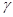 обозначим через
обозначим через  и назовем централизатором фактора
и назовем централизатором фактора  в
в 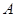 .
.
Напомним, что факторы  и
и 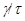 назыавются перспективными, если либо
назыавются перспективными, если либо

либо
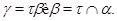
Докажем основные свойства централизаторов конгруэнции.
Теорема 6 Пусть 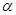 ,
,  ,
, 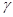 ,
, 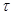 – конгруэнции на алгебре
– конгруэнции на алгебре  . Тогда:
. Тогда:
1) если  , то
, то

2) если  , то
, то
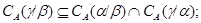

3) если  ,
,  и факторы
и факторы  ,
, 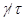 перспективны, то
перспективны, то
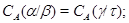
4) если  – конгруэнции на
– конгруэнции на  и
и  , то
, то

где 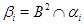 ,
,  .
.
Доказательство.
1) Так как конгруэнция  централизует любую конгруэнцию и
централизует любую конгруэнцию и  , то
, то

2) Из первого пункта лемы 2.2 следует, что

а в силу леммы 2.4 получаем, что

Пусть  – изоморфизм
– изоморфизм  . Обозначим
. Обозначим

По лемме 2.5  , а по определению
, а по определению

Следовательно,

3) Очевидно, достаточно показать, что для любых двух конгруэнции  и
и  на алгебре
на алгебре  имеет место равенство
имеет место равенство
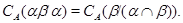
Покажем вналале, что

Обозначим  . Тогда, согласно определению 2.1. на алгебре
. Тогда, согласно определению 2.1. на алгебре  существует такая конгруэнция
существует такая конгруэнция 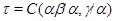 , что выполняются следующие свойства:
, что выполняются следующие свойства:
а) если  , то
, то
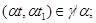
б) для любого элемента  ,
,

в) если


то

Построим бинарное отношение  на алгебре
на алгебре  следующим образом:
следующим образом:

тогда и только тогда, когда
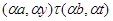
и

Покажем, что  – конгруэнция на
– конгруэнция на  . Пусть
. Пусть

для  . Тогда
. Тогда

и

Так как  – конгруэнция, то для любой
– конгруэнция, то для любой  -арной операции
-арной операции  имеем
имеем

Очевидно, что
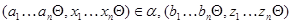
и
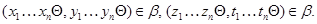
Следовательно,

Очевидно, что для любой пары 

Значит,
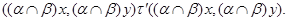
Итак, по лемме 2.3,  – конгруэнция на
– конгруэнция на 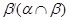 . Покажем теперь, что
. Покажем теперь, что  удовлетворяет определению 2.1, то есть
удовлетворяет определению 2.1, то есть  централизует
централизует  . Пусть
. Пусть
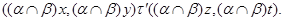
Тогда

Так как 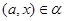 ,
,  и
и  , то
, то 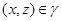 . Следовательно,
. Следовательно,  удовлетворяет определению 2.1.
удовлетворяет определению 2.1.
Если 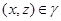 , то
, то

значит,

Пусть, наконец, имеет место (1) и

Тогда 
Так как  и
и  , то
, то  , следовательно,
, следовательно,  . Из (2) следует, что
. Из (2) следует, что  , а по условию
, а по условию 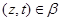 . Значит,
. Значит, 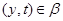 и поэтому
и поэтому

Тем самым показано, что конгруэнция  удовлетворяет определению 2.1, то есть
удовлетворяет определению 2.1, то есть  централизует
централизует  .
.
Докажем обратное включение. Пусть
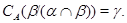
Тогда на алгебре  определена конгруэнция
определена конгруэнция

удовлетворяющая определению 2.1. Построим бинарное отношение  на алгебре
на алгебре  следующим образом:
следующим образом:

тогда и только тогда, когда

и 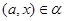 ,
, 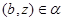 .
.
Аналогично, как и выше, нетрудно показать, что  – конгруэнция на алгебре
– конгруэнция на алгебре  . Заметим, что из доказанного включения в одну сторону следует, что
. Заметим, что из доказанного включения в одну сторону следует, что  . Покажем поэтому, что
. Покажем поэтому, что 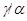 централизует
централизует  .
.
Так как



то

то есть  удовлетворяет условию 1) определения 2.1.
удовлетворяет условию 1) определения 2.1.
Если 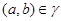 , то
, то
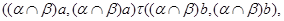
следовательно,

Пусть имеет место (3) и  .
.
Так как

то

Из (4) следует, что  , следовательно,
, следовательно,

то есть

На основании леммы 2.2 заключаем, что

Следовательно,  .
.
А так как  , то
, то  , то есть
, то есть

4) Обозначим  . Пусть
. Пусть

и удовлоетворяет определению 2.1.
Определим бинарное отношение  на
на  следующим образом
следующим образом
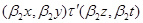
тогда и только тогда, когда
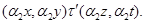
Аналогично, как и выше, нетрудно показать, что  – конгруэнция, удовлетворяющая определению 2.1.
– конгруэнция, удовлетворяющая определению 2.1.
Это и означает, что
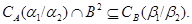
Теорема доказана.
Как следствия, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.
 2020-01-14
2020-01-14 90
90








