Этап 6. Определение лица (или группы лиц), принимающих решение

Для проведения исследования была выбрана группа экспертов, состоящая из сотрудников АО «Самаравтормет» (внутренние эксперты) и специалистов, приглашённых со стороны (аудитор, финансовый аналитик, независимый эксперт).

В состав экспертной группы вошли:

1. Генеральный директор АО «Самаравтормет»

2. Зам. Генерального директора

3. Главный бухгалтер

4. Начальник планово-экономического отдела

5. Аудитор

6. Финансовый аналитик

7. Начальник кадрового отдела

8. Независимый эксперт (я)

Все приглашенные эксперты являются специалистами высокого уровня, они обладают широким кругозором, достаточно эрудированны как в узких, так и в смежных областях.

Им было предложено ответить на следующие вопросы:

1. Можно ли за короткий срок решить указанную проблему?

2. Сможет ли просуществовать предприятие ближайшие два года без основательных капиталовложений?

3. Имеются ли сегодня предпосылки по расширению связей с потенциальным кругом поставщиков?

4. Поможет ли использование новой техники и передовых технологий коренным образом улучшить положение дел?

5. Поможет ли совершенствование организационной структуры управления решению основной проблемы?

6. Велико ли на самом деле влияние конкурирующих фирм при распределении сфер деятельности?

Таблица 1 – Варианты ответов экспертов по основным вопросам

Вопросы Эксперты	1	2	3	4	5	6	P	q	σ^2
I	1	0	1	1	0	1	0,7	0,3	0,21
II	1	1	0	0	1	1	0,7	0,3	0,21
III	1	0	0	1	1	0	0,5	0,5	0,25
IV	0	0	1	1	0	1	0,5	0,5	0,25
V	1	0	1	1	1	0	0,7	0,3	0,21
VI	1	0	0	0	1	1	0,5	0,5	0,25
VII	0	1	1	0	1	1	0,7	0,3	0,21
VIII	0	1	1	0	1	0	0,5	0,5	0,25

Р= ,

где М – число единиц (положительные ответы);

N – общее число параметров.

q= , где L – число нулей (отрицательные ответы)

p+q = 1

Дисперсия, характеризующая отклонение от средней величины определяется: σ²=P*q

Проведем классификацию ответов экспертов, используя приемы таксономии, для этого определяем коэффициент близости между ответами. Воспользуемся формулой Роджерса и Танимото

S = (n^(1;1)_i_,_j)/(n⁽¹⁾_i + n⁽¹⁾_j – n^(1;1)_i_,_j),

Где n^(1;1)_i_,_j – число совпадающих единиц между сравниваемыми рядами.

n⁽¹⁾_i – число всех единиц в i – том сравниваемом году

n⁽¹⁾_j – число единиц в j – том сравниваемом ряду.

S = 2/(4+4-2) = 0,33- коэффициент близости между ответами I и II экспертов

S = 2/(4+3-2) = 0,4- коэффициент близости между ответами I и III экспертов

……….

Сравнивая первый ряд последовательно со всеми остальными, заполняется первая строка матрицы, затем вторая строка со всеми остальными и т.д. В результате получим матрицу (табл.2).

Таблица 2 – Определение коэффициентов близости между ответами экспертов

	I	II	III	IV	V	VI	VII	VIII
I	-	0,33	0,4	0,75	0,6	0,4	0,33	0,17
II	0,33	-	0,4	0,17	0,33	0,75	0,6	0,4
III	0,4	0,4	-	0,2	0,75	0,5	0,17	0,2
IV	0,75	0,17	0,2	-	0,4	0,2	0,4	0,2
V	0,6	0,33	0,75	0,4	-	0,4	0,33	0,4
VI	0,4	0,75	0,5	0,2	0,4	-	0,4	0,2
VII	0,33	0,6	0,17	0,4	0,33	0,4	-	0,75
VIII	0,17	0,4	0,2	0,2	0,4	0,2	0,75	-

0,75

0,4

0,75

0,4

0,75

0,6

0,75

После обработки данной таблицы получаем граф:

Итак, мнение экспертов можно представить следующим образом:

S (коэффициент близости) P

0,75 - III, IV, V, VI, VIII I – 0,3

0,6 – I II – 0,3

0,4- II,, VII III – 0,5

IV – 0,5

V – 0,7

VI – 0,5

VII – 0,7

VIII – 0,5

Эти данные позволят нам составить следующий график:

VIII

VII

III

Таксоны формировались по коэффициентам близости, получилось 2 таксона. Это говорит о наличии двух групп мнений. В первый таксон входят эксперты: II, I, VII. Причём, следует отметить, что эксперт I – генеральный директор находится практически по середине между двумя группами (расстояние до первого таксона не намного меньше, чем до второго, поэтому всё-таки я отнесла его к первому таксону). Т.е. можно сказать, что генеральный директор выслушав оба мнения, примет единственно верное решение. Он как бы не примыкает ни к одной из групп, держит нейтралитет. Поэтому можно сказать, что в первый таксон входит только два эксперта: заместитель генерального директора и начальник отдела кадров. Во второй таксон входят эксперты: III, IV, V, VI, VIII. Во втором таксон входят: главный бухгалтер, начальник планово-экономического отдела, аудитор, финансовый аналитик и независимый эксперт. Получается, что, во-первых, во второй таксон входит большее число экспертов. Во-вторых, в него входят те специалисты, которые хорошо изучили именно финансовые ресурсы, возможности предприятия на данный момент. Поэтому я буду опираться при выборе решения на второй таксон.

Ознакомившись с проектной документацией, эксперты предложили свои варианты расчетов, основываясь на благоприятном (Kmin) и неблагоприятном (Kmax) прогнозах. Посоветовавшись с главным бухгалтером, я приняла его точку зрения. Результаты их прогнозов представлены в таблице 4:

Эксперты	Значения характеристик дополнительных капиталовложений (млрд. руб.)
Эксперты	Вариант 1 (K^min)	Вариант 2 (K^max)
I	0,5	0,6
II	0,3	0,4
III	0,5	0,7
IV	0,2	0,4
V	0,4	0,6
VI	0,5	0,6
VII	0,3	0,4
VIII	0,5	0,4

Далее представлены меры близости мнений экспертов (таблица 5):

Для нахождния коэффициентов близости используется евклидово расстояние.

d_ij = (

d₁₂ = (0.5-0.3)^2+(0.6-0.4)^2 = 0.28

d₁₃ = (0.5-0.5)^2+(0.6-0.7)^2 = 0.1

……

Таблица 5 – Коэффициенты близости мнений экспертов

	I	II	III	IV	V	VI	VII	VIII
I	-	0,28	0,1	0,36	0,1	0	0,28	0,2
II	0,28	-	0,36	0,1	0,22	0,28	0	0,2
III	0,1	0,36	-	0,42	0,14	0,1	0,36	0,3
IV	0,36	0,1	0,42	-	0,28	0,36	0,1	0,3
V	0,1	0,22	0,14	0,28	-	0,1	0,22	0,22
VI	0	0,28	0,1	0,36	0,1	-	0,28	0,2
VII	0,28	0	0,36	0,1	0,22	0,28	-	0,2
VIII	0,2	0,2	0,3	0,3	0,22	0,2	0,2	-

После обработки данной таблицы получаем граф:

0,42

0,36

0,28

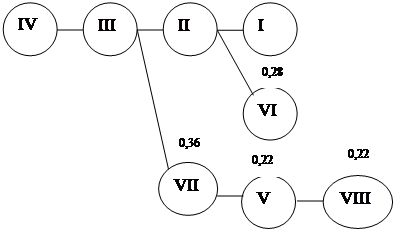
Итак, мнение экспертов можно представить следующим образом:

S (коэффициент близости) K^max

0,42 – III, IV I – 0,6

0,36 – II, VII II – 0,4

0,28 – I, VI III – 0,7

0,22 – V, VIII IV – 0,4

V – 0,6

VI – 0,6

VII – 0,4

VIII – 0,4

K^max, млрд. руб.

Эти данные позволяют построить нам следующий график:

VIII

VII

III

Таксоны формировались по коэффициентам близости, получилось 2 таксона. Это говорит о наличии двух групп мнений. При этом в каждом из таксонов объединилось одинаковое количество экспертов (по 4 человека). В первый таксон входят: генеральный директор, аудитор, финансовый аналитик, независимый эксперт. Во второй таксон входят: заместитель генерального директора, главный бухгалтер, начальник планово-экономического отдела и начальник отдела кадров. По мнению, специалистов из первого таксона, АО «Самаравтормет» нуждается в дополнительных капиталовложениях в среднем в размере 0,5 млрд. руб. Специалисты, входящие во второй таксон, считают, что предприятию необходимы капиталовложения в больших размерах: 0,55 млрд. руб. (в среднем). Я считаю, что нужно ориентироваться на мнение второго таксона, так как в него входит главный бухгалтер, который озвучил цифру 0,7 млрд. руб. Потому что именно бухгалтер ведёт всю финансовую отчётность предприятия и имеет представление о количестве основных средств, о финансовых ресурсах организации и т.д. Остальные эксперты, входящие во второй таксон озвучили цифру 0,4 млрд. руб. Но с мнением главного бухгалтера нельзя не считаться, поэтому возьмём среднюю цифру – 0,55 млрд. руб. Причём эта сумма близка к сумме, которая необходима, по мнению специалистов, входящих в первый таксон. Значит, в этом вопросе особых расхождений быть не должно.