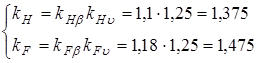 ,
,
где 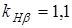 и
и 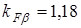 - коэффициенты неравномерности распределения нагрузки по длине контактных линий
- коэффициенты неравномерности распределения нагрузки по длине контактных линий  ;
;
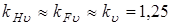 - коэффициенты динамичности нагрузки
- коэффициенты динамичности нагрузки 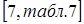 .
.
Определение среднего диаметра шестерни по начальному (делительному) конусу
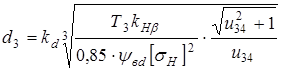
где 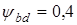 по
по 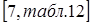 - коэффициент ширины шестерни относительно ее диаметра;
- коэффициент ширины шестерни относительно ее диаметра;
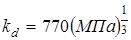 - для стальных колес при 20-градусном зацеплении без смещения рекомендуется принимать при расчете прямозубых конических передач.
- для стальных колес при 20-градусном зацеплении без смещения рекомендуется принимать при расчете прямозубых конических передач.
Вращающий момент на валу колеса:
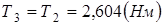 .
.
Таким образом,
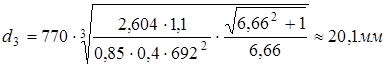 .
.
Из конструктивных соображений принимаем 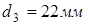 .
.
Определение модуля в среднем сечении зуба, конусного расстояния и внешнего окружного модуля
Модуль в среднем сечении зуба
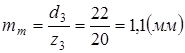 .
.
Конусное расстояние
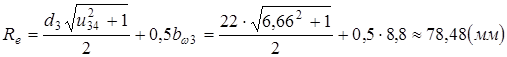 ,
,
где 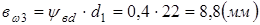 - ширина зубчатого венца.
- ширина зубчатого венца.
Внешний окружной модуль
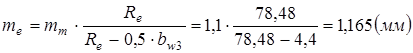
Округляя это значение до ближайшего стандартного по ГОСТ9563-60, получаем 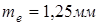 .
.
Уточняем 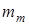 и
и 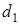 :
:
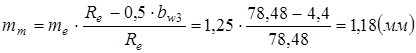 ;
;
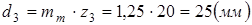
Проверочный расчет
Проверка передачи на контактную выносливость
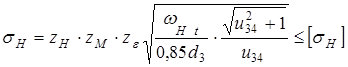 ,
,
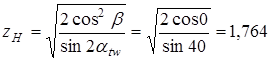
- коэффициент, учитывающий форму сопряженных поверхностей зубьев;
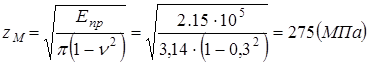
- коэффициент, учитывающий механические свойства материалов сопряженных колес;
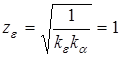
- коэффициент, учитывающий суммарную длину контактных линий.
Уточняем окружную скорость:
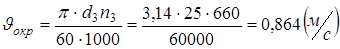 .
.
Уточняем коэффициент расчётной нагрузки:
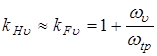 ,
,
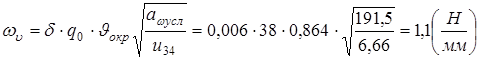
- удельная окружная динамическая сила;
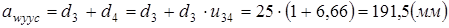
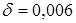 - коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев;
- коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев;
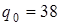 - коэффициент, учитывающий влияние разности основных шагов зацепления зубьев шестерни и колеса;
- коэффициент, учитывающий влияние разности основных шагов зацепления зубьев шестерни и колеса;
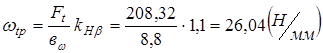
- удельная расчётная окружная сила в зоне наибольшей концентрации;
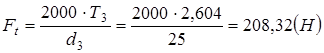
- полезная окружная сила.
Cследовательно,
 ;
;
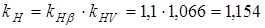 ;
;
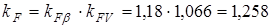 .
.
Определю удельную расчётную окружную силу:
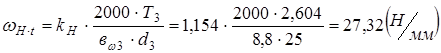 ,
,
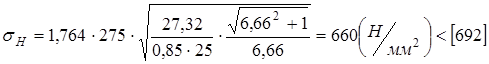 ,
,
таким образом, недогрузка 3,2%.
Проверка зубьев передачи на изгибную выносливость
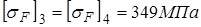
Определю коэффициенты формы зубьев шестерни и колеса:
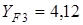 для
для 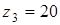
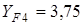 для
для 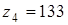
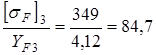 ,
, 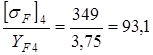 ,
,
так как 84,7<90,6 проверяем зуб шестерни:
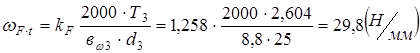 .
.
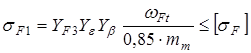 ,
,
где 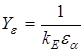 - коэффициент, учитывающий перекрытие зубьев, при 5-й степени точности
- коэффициент, учитывающий перекрытие зубьев, при 5-й степени точности
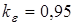 ;
; 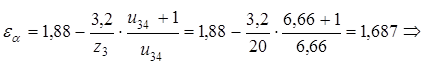
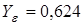 ;
;
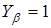 - коэффициент, учитывающий наклон зубьев
- коэффициент, учитывающий наклон зубьев
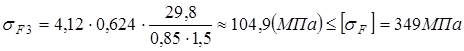 .
.
Определение геометрических и других размеров колеса и шестерни
Половины углов при вершинах делительных (начальных) конусов шестерни и колеса находим из равенства
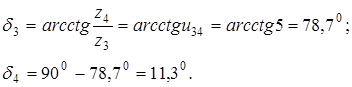
Конусное (дистанционное) расстояние 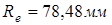 .
.
Диаметры вершин зубьев по большому торцу равны:
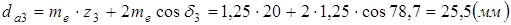 ;
;
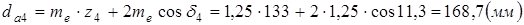 .
.
Диаметры окружностей впадин по большому торцу равны:
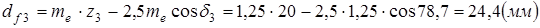 ;
;
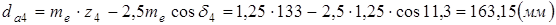 .
.
Углы головок и ножек зубьев шестерни и колеса соответственно равны
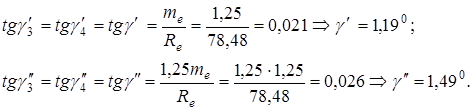
Половины углов конусов вершин зубьев (конусность заготовок) шестерни и колеса соответственно равны:
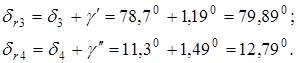
Определяем диаметр отверстия под вал в колесе:
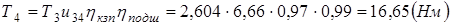 ,
,
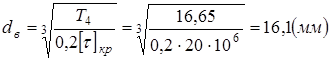 ,
,
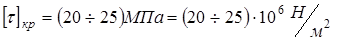 .
.
Принимаем из конструктивных соображений 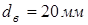 .
.
 2020-01-14
2020-01-14 162
162








