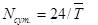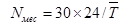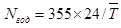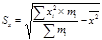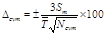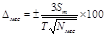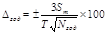себестоимость рентабельность производительность планирование
Задание:
На основе статистических данных, приведенных в табл.9, определить:
1. Среднюю продолжительность (Т) плавки металла в агрегате, норму производительности агрегата (число плавок) в сутки (Nсут), в год (Nгод), и возможные относительные максимальные погрешности при определении этих норм.
2. Уравнение регрессии, отражающее зависимость продолжительности плавки агрегате (Т1) от величины фактора (х1), а также величину коэффициента корреляции (r) оценивающего тесноту связи Т1=f(х1). Составить таблицу нормативных значений Т.
Примечание: При расчете производительности агрегата принять продолжительность месяца, равную 30 суткам, а фактическое время работы агрегата за год – 355 суток.
Для осуществления статистических расчетов необходимо составить табл.2. По горизонтали таблицы приводятся значения фактора (х1), а по вертикали – значения продолжительностей плавок (Т1). На пересечении этих показателей приводится число плавок (m1).
1. Рассчитать средневзвешенную продолжительность плавки металла в агрегате:
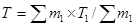 (2)
(2)
2. Планируемое число плавок составит:
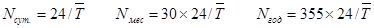 (3)
(3)
3. Среднеквадратичное отклонение для ряда распределения продолжительностей плавки (Ti) рассчитаем по формуле:
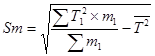 (4)
(4)
4. Относительные максимальные погрешности при планировании числа плавок: в сутки, в месяц, в год.
5. По данным табл.ниже строят эмпирическую линию регрессия в виде ломанной линии (см. рис. ниже). Очевидно, что зависимость между продолжительностью плавки (Тi) и решающим фактором (xi) может быть выражена прямой линией:
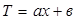
Величину коэффициента корреляции r и других статистических характеристик рассчитаем по формулам, известным по курсам статистики:
Свободный член «в» в уравнении регрессии равен
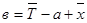
нормирование труд хронометражный сменность
Подставляя найденные значения параметров «а» и «в» в уравнение регрессии получим эмпирическую зависимость продолжительности плавки (Тi) от решающего фактора (хi).
Строим графики теоретической и эмпирической линий регрессии согласно уравнению и исходным данным.
Расчет задания 4 представлен ниже в таблицах 13,14 и 15.
Таблица 14 – Расчет параметров уравнения корреляционной зависимости
| Коэффициенты уравнения | Расчет | Значение |
| а | 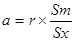
| 0,0768 |
| b | 22,6369 | |
| r | 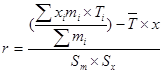
| 0,9699 |
| Sx | 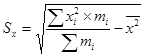
| 122,7021 |
| хср | 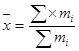
| 511,9383 |
Примечание: где r – коэффициент корреляции, характеризующий тесноту связи зависимости Тi = f(xi).
Таблица 13 – Расчет теоретических данных числа плавок
Исходные данные | Расчетные данные | |||||||||||
| Тi∙mi | Т2i | Т2i∙mi | хi∙mi | хi∙Тi | хi2 | хi2∙mi | хi∙mi∙Тi | Тiтеор. | ||||
| Продо-лжи-тель-ность плавок Тi | число плавок mi | Значение фактора xi | ||||||||||
| 40 | 2 | 280 | 80 | 1600 | 3200 | 560 | 11200 | 78400 | 156800 | 22400 | 44,13 | |
| 37 | 6 | 330 | 222 | 1369 | 8214 | 1980 | 12210 | 108900 | 653400 | 73260 | 47,97 | |
| 49 | 10 | 370 | 490 | 2401 | 24010 | 3700 | 18130 | 136900 | 1369000 | 181300 | 51,04 | |
| 51 | 40 | 430 | 2040 | 2601 | 104040 | 17200 | 21930 | 184900 | 7396000 | 877200 | 55,65 | |
| 64 | 38 | 480 | 2432 | 4096 | 155648 | 18240 | 30720 | 230400 | 8755200 | 1167360 | 59,49 | |
| 61 | 70 | 530 | 4270 | 3721 | 260470 | 37100 | 32330 | 280900 | 19663000 | 2263100 | 63,33 | |
| 74 | 34 | 580 | 2516 | 5476 | 186184 | 19720 | 42920 | 336400 | 11437600 | 1459280 | 67,17 | |
| 71 | 16 | 630 | 1136 | 5041 | 80656 | 10080 | 44730 | 396900 | 6350400 | 715680 | 71,01 | |
| 76 | 8 | 680 | 608 | 5776 | 46208 | 5440 | 51680 | 462400 | 3699200 | 413440 | 74,85 | |
| 89 | 3 | 730 | 267 | 7921 | 23763 | 2190 | 64970 | 532900 | 1598700 | 194910 | 78,69 | |
| 612 | 227 | 5040 | 14061 | 40002 | 892393 | 116210 | 330820 | 2749000 | 61079300 | 7367930 |
| |
| 61,94 | 22,7 | 512 |
|
|
|
|
|
|
|
|
| |
Таблица 15 – определение норм производительности агрегата
| Показатели | Расчет | Результат |
| Плановое число плавок |
|
|
| В сутки |
| 0,39 |
| В месяц |
| 11,62 |
| В год |
| 137,55 |
| Среднеквадратичное отклонение |
| 9,7131 |
| Относительные погрешности |
|
|
| В сутки |
| 0,2928 |
| В месяц |
| 1,6038 |
| В год |
| 5,5171 |
Ниже представлено графическое изображение эмпирической и теоретической линии регрессии.
 2020-01-14
2020-01-14 162
162