Построение эпюр поперечных сил, изгибающих и приведенных моментов

При определении закона распределения поперечных сил и изгибающих моментов по длине крыла вначале находим функции  и  от воздействия распределенной нагрузки . Для этого табличным способом вычисляем интегралы методом трапеций.

 

,                ,

 

Расчет производим по следующим формулам:

 

;

; ,

, .

 

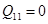Аналогично рассчитываем величины изгибающих моментов:

 

; ;

,

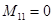Полученные результаты заносим в таблицу 2.

 

Таблица 2

	z, м	ΔQ, кг	Q, кг	ΔM, кгм	M, кгм
0	0	2244,77	20592,41	196758,3	1016728
0,1	1,462	2690,34	18347,64	172115,8	819969,8
0,2	2,924	2969,13	15657,30	152033,9	647854
0,3	4,386	3127,09	12688,17	130883,4	495820,1
0,4	5,848	3194,27	53414,20	121865,8	364936,7
0,5	7,31	3167,01	43712,46	87477,02	243070,9
0,6	8,772	3068,96	34081,88	66035,43	155593,9
0,7	10,234	2895,33	24644,21	57833,87	89558,46
0,8	11,696	2595,34	15538,14	24598,34	31724,59
0,9	13,158	1602,68	6337,4565	7126,248	7126,248
1	14,62	0	0	0	0

 

Необходимо учесть воздействие сосредоточенных массовых сил :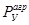

 

(кг);

, ;

,

 

Построим эпюры ,  (рис. 8)

 

Рис. 8

 

При построении эпюры приведенных моментов вначале задаемся положением оси приведения. Она проходит через переднюю кромку крыла параллельно оси “z” Строим эпюру погонных моментов  от воздействия распределенных нагрузок 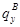,  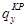и .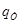

Для погонных моментов:

 

,

 

где

 

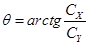, тогда

.

 

 - расстояния от точек приложения нагрузок  до оси приведения.

 

,

 

 

.

 

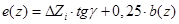Момент считаем положительным, если он действует против часовой стрелки.

Интегрируя эпюру , получаем приведенные моменты  от воздействия распределенных нагрузок. Схема расчета имеет вид:

 

;

.

 

Полученные результаты заносим в таблицу 3:

Таблица 3

qv	qkr	qt	av	akr	at	mz	dM	M
4027,11	502,72	2187,44	1,67127	2,2185	2,3664	438,75654		42399,48
4032,53	464,88	1870,60	1,69219	2,1982393	2,335009	1434,007	1368,9901	41030,49
3952,09	427,05	1578,54	1,713111	2,1779786	2,303619	2203,8936	2659,3053	38371,18
						5840,2499
3779,82	389,22	1311,25	1,734031	2,1577179	2,272228	6371,3749	3610,3448	34760,84
3584,23	351,39	1068,74	1,754951	2,1374572	2,240837	6780,5438	4297,6997	30463,14
						3144,1876
3337,71	313,56	851,01	1,775871	2,1171965	2,209446	3383,2196	4771,5346	25691,6
3062,89	275,73	658,05	1,796792	2,0969357	2,178056	3491,9366	5025,7392	20665,86
2769,34	237,90	489,86	1,817712	2,076675	2,146665	3488,2576	5102,522	15563,34
2440,94	200,07	346,45	1,838632	2,0564143	2,115274	3343,7442	4994,1933	10569,15
2024,72	162,24	227,82	1,859553	2,0361536	2,083884	2959,9915	4608,0307	5961,119
1542,45	143,32	177,79	1,870013	2,0260233	2,068188	2226,3231	3791,1959	2169,923
0,00	0,00	0,00	1,880473	2,0158929	2,052493	0	2169,9229	0

 

Приведенный момент от воздействия сосредоточенных масс находим по формуле:

 

,

 

где  - расстояние от цеyнтра тяжести -того бака до оси приведения.

 

 

Строим суммарную эпюру  (рис. 9)

 

 

Рис. 9

Проверка правильности построения эпюр нагрузок по крылу.

 

 

С эпюры =20592кг.

 

 

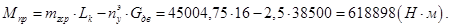
Определение точки положения поперечной силы в расчетном сечении

Зная поперечную силу и приведенный момент в расчетном сечении( =0.2), можно найти точку приложения поперечной силы по хорде крыла расчетного сечения:

 

 

Координату  откладывают от оси приведения.