План
· Інтегрування частинами
· Інтегрування часток
· Заміна змінної
Інтегрування частинами
Нехай 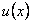 і
і  – диференційовані функції
– диференційовані функції  на
на 
Тоді 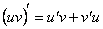 або
або

Звідси
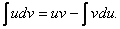 (8.16)
(8.16)
Формула (8.16) називається формулою інтегрування частинами в невизначеному інтегралі.
Користуючись формулою (8.16), рекомендується обчислення інтегралів від таких функцій:

де 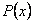 –поліном,
–поліном, 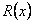 – раціональна функція
– раціональна функція  . Описати всі можливі випадки застосування формули інтегрування частинами неможливо. Інтегруючи такі вирази, завжди виникає дилема: що взяти за
. Описати всі можливі випадки застосування формули інтегрування частинами неможливо. Інтегруючи такі вирази, завжди виникає дилема: що взяти за  , а що – за
, а що – за  . Інтегруючи вирази вигляду
. Інтегруючи вирази вигляду  ,
,  , після того як підінтегральна функція буде розписана за властивостями 40 і 50, одержимо інтеграли вигляду
, після того як підінтегральна функція буде розписана за властивостями 40 і 50, одержимо інтеграли вигляду  , де
, де  - одна з функцій
- одна з функцій  в яких слід за
в яких слід за  брати
брати 
 , бо, в протилежному випадку, інтеграл ускладнюватиметься за рахунок зростання степенів
, бо, в протилежному випадку, інтеграл ускладнюватиметься за рахунок зростання степенів  . В інтегралах
. В інтегралах  , де
, де  - одна з функцій
- одна з функцій  вигідно за
вигідно за  брати
брати  . В інших випадках вибір
. В інших випадках вибір  здійснюється залежно від того, при якому з виборів легше знайти
здійснюється залежно від того, при якому з виборів легше знайти  за
за  , хоч це теж не є абсолютною істиною. Іноді доводиться експериментувати.
, хоч це теж не є абсолютною істиною. Іноді доводиться експериментувати.
Інтегруючи вирази  , доцільно за
, доцільно за  взяти
взяти  . Знаходження
. Знаходження  із співвідношень
із співвідношень  теж здійснюється інтегрування частинами.
теж здійснюється інтегрування частинами.
Для прикладу знайдемо

Приймаючи  , а
, а  , знайдемо
, знайдемо
 Далі матимемо
Далі матимемо  , тобто дістанемо інтеграл
, тобто дістанемо інтеграл  .
.
Знову, взявши  , знайдемо
, знайдемо  . Отже, одержимо таку систему рівнянь відносно
. Отже, одержимо таку систему рівнянь відносно  та
та  :
:

Звідси


Приклад 1.

Позначивши  ,
,
одержимо  . Звідси
. Звідси
 . (8.17)
. (8.17)
Остання формула є рекурентною, тобто, знаючи, що  , можна поступово знайти
, можна поступово знайти  , де
, де  – ціле число,
– ціле число,
більше за одиницю. Наприклад, при 

Звідси  .
.
Приклад 2. 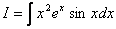 .
.
Нехай  Тоді
Тоді
 і
і
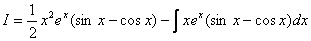
У новому інтегралі степінь величини понизився на одиницю, а це означає, що інтеграл став простішим, ніж був.
Знайдемо тепер 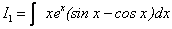 . Маємо
. Маємо  .
.
Звідси 
Отже, на основі формули (8.16) одержимо
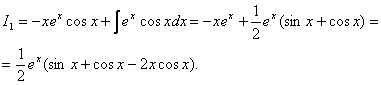
Враховуючи значення  , знаходимо
, знаходимо
 .
.
Приклад 3.


Із останньої рівності одержимо
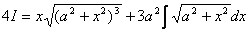 .
.
Обчислимо тепер
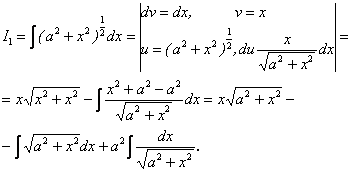
Звідси  .
.
Остаточно з урахуванням  , матимемо
, матимемо
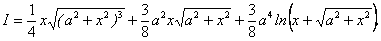
Останній приклад показує, що часто інтегрування частинами приводить до мети скоріше в тих випадках, де, як це здавалось би, доцільніше застосувати інші методи. У цьому можна переконатися, спробувавши знайти первісну для функції  , застосувавши наприклад, заміну змінної за формулою
, застосувавши наприклад, заміну змінної за формулою  , про що мова буде іти пізніше.
, про що мова буде іти пізніше.
Інтегрування часток
Через те, що  то
то
 . (8.18)
. (8.18)
Користуючись цим, стають очевидними такі формули:
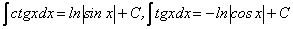 .
.
Нехай маємо 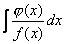 , причому
, причому  , де
, де  – довільне дійсне число. Тоді
– довільне дійсне число. Тоді
 .
.
Розглянемо інтеграл вигляду 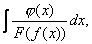 якщо
якщо  , то
, то

 , (8.19)
, (8.19)
де  .
.
Приклади.
1.  .
.
2.  .
.
3. 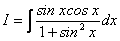 .
.
Через те що  , то
, то
 .
.
Заміна змінної
Нехай потрібно обчислити інтеграл 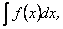 причому безпосередньо первісну ми знайти не можемо, але відомо, що вона існує.
причому безпосередньо первісну ми знайти не можемо, але відомо, що вона існує.
Зробимо заміну змінної в підінтегральному виразі
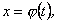
де  неперервна функція з неперервною похідною, що має обернену функцію. Тоді
неперервна функція з неперервною похідною, що має обернену функцію. Тоді  і в цьому випадку має місце формула
і в цьому випадку має місце формула
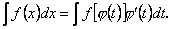 (8.20)
(8.20)
Формулу (8.20) слід розуміти так, що після інтегрування в правій частині рівності замість  буде підставлено його вираз через
буде підставлено його вираз через 
Щоб довести рівність (8.20), потрібно довести, що похідні за  від обох частин рівності рівні між собою:
від обох частин рівності рівні між собою:
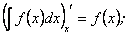

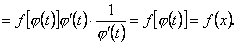
Ми тут використали правило диференціювання оберненої функції.
Отже, похідні за  від обох частин рівності (8.20) рівні, що й треба було довести.
від обох частин рівності (8.20) рівні, що й треба було довести.
Функцію 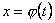 потрібно вибирати так, щоби можна було обчислити інтеграл, що стоїть в правій частині рівності (8.20).
потрібно вибирати так, щоби можна було обчислити інтеграл, що стоїть в правій частині рівності (8.20).
Фактично у п. 9.3.5 теж йшлося про заміну змінної, в чому можна безпосередньо переконатися.
Не можна дати універсальних замін змінних, які зводили б заданий інтеграл до простішого. Але для ряду випадків це можна здійснити. Доцільно, наприклад, в інтегралах, що містять під знаком інтеграла вирази вигляду 
застосувати відповідно такі заміни змінних:  або
або 

 або
або  .
.
За подальшого вивчення методів інтегрування розглядатимуться інші заміни змінних.
Приклади.
1.  . Підстановка
. Підстановка  зводить інтеграл до такого:
зводить інтеграл до такого:
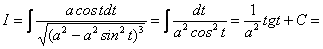

2.  . Щоб позбутися експонент, доцільно скористатися такою заміною змінної
. Щоб позбутися експонент, доцільно скористатися такою заміною змінної  .Тоді
.Тоді  і інтеграл набере вигляду
і інтеграл набере вигляду
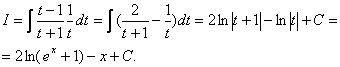
 2020-04-20
2020-04-20 165
165






