Статистическая проверка гипотез

1. Пусть случайная величина X~N(a, ), причем параметры распределения неизвестны.

а) Проверим нулевую гипотезу H₀: для , если альтернативная гипотеза H₁: .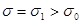

 Найдем наблюдаемое значение критерия:

.

По условию конкурирующая гипотеза имеет вид первого случая, поэтому критическая область правостороння, по уровню значимости равному 0,05 и числу степеней свободы 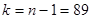, находим критическую точку , при . Так как 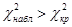 – есть основание отвергнуть гипотезу.

б) Далее проверим следующую нулевую гипотезу 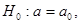если альтернативная гипотеза . Уровень значимости принимается

Для этого вычислим наблюдаемое значение критерия:

По таблице критических точек распределения Стъюдента имеем:

Т.е. получилось, что , следовательно, нулевая гипотеза