2020-04-20
150
Проводим снизу от схемы редуктора горизонтальную прямую. Вдоль оси 
проводим вертикальную линию до пересечения с горизонтальной прямой. На пересечении получаем точку 
.
Проводим из точки А колеса 1 вертикальную линию до пересечения с горизонтальной прямой. От точки пересечения перпендикулярно откладываем в масштабе 
вектор скорости точки А (
):
Соединяем конец вектора с точкой , получаем картину распределения скоростей колеса 1. Для построения картины распределения скоростей для колес 2 и 2’ соединяем конец вектора с точкой 
. Для нахождения скорости точки 
, на уровне точки восстанавливаем перпендикуляр к горизонтальной прямой до пересечения с прямой 
. Величина перпендикуляра в масштабе дает нам модуль скорости.
Аналогично определяем законы распределения скоростей для остальных колес.
Для построения плана угловых скоростей проведем две линии: горизонталь и вертикаль. На вертикальной линии отложим масштабе значение угловой скорости первого колеса 
(точка 1). Из точки 1 проводим прямую, параллельную линии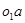 
(линии, выражающей закон распределения скоростей для первого колеса). На пересечении этой линии с горизонтальной прямой получим полюс построения Н. Проводим из полюса прямые параллельные линиям, выражающим законы распределения скоростей для всех колес, и получаем в пересечении с горизонтальной прямой точки 2, 3 и т. д. Отрезки [01], [02] и т. д. будут в масштабе давать угловые скорости колес.
Масштабный коэффициент
Определяем угловые скорости колес. Данные расчета приведены в таблице 3.2
Передаточное отношение редуктора определим из плана угловых скоростей
Таблица 3.2
| Колесо | Отрезок, мм | Угловая скорость, с-1 |
| 1 | 150 | 3 |
| 2 | 141,66 | 2,8332 |
| 4 | 44,44 | 0,8888 |
| 5 | 111,11 | 2,2222 |
| 7 | 40,4 | 0,808 |
| 8 | 33,67 | 0,6734 |
Сравнение результатов кинематического анализа
Сравниваем передаточные отношения, найденные аналитическим и графическим способами.
