2020-04-07
1206Раздел 2. ТЕОРИЯ БАЛОЧНОГО КОНЕЧНОГО ЭЛЕМЕНТА
Балочный конечный элемент обладает свойствами, которые характерны для балки – элементарной расчетной схемы, сопротивляющейся изгибу и сдвигу в плоскости поперечного сечения. При этом балка полагается недеформируемой вдоль своей оси, а также имеющей недеформируемое поперечное сечения, геометрические характеристики которого вдоль оси также не изменяются.
Перемещения и деформации такой балки при плоском изгибе определены как малые (рис. 11), а НДС балки полностью определяется величиной поперечного прогиба оси балки, проходящей через центры тяжести ее сечений. Расчет при этом ведется по недеформированной схеме.
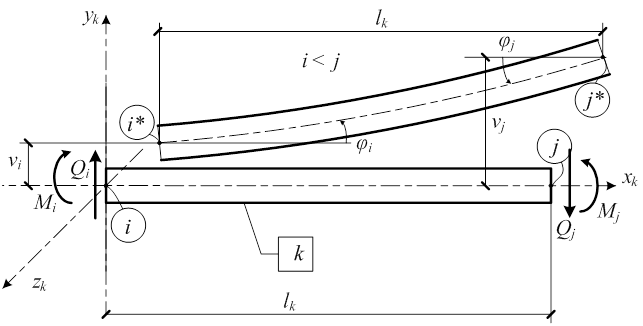
Рис. 11. Балочный конечный элемент
Отметим, наконец, что все последующие построения для балочного конечного элемента по последовательности и характеру действий не отличаются от построений для стержневого КЭ.
4.1. Построение матрицы интерполяционных функций прогиба в сечениях балочного конечного элемента
|
|
|
Рассмотрим НДС балочного КЭ в ЛСК под действием усилий, приложенных в узловых сечениях КЭ и обеспечивающих его равновесие (см. рис. 11).
Деформированное состояние балки однозначно определено её поперечными прогибами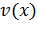 
и углами поворота сечений 
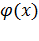, которые, будучи малыми, вычисляются как 
.
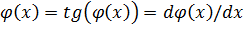Предложим форму функции связи между осевым перемещением произвольного сечения КЭ и перемещениями в узловых сечениях в виде полинома третьей степени, поскольку он определяется 4-я параметрами, что соответствует 4-м степеням свободы балочного КЭ в его узлах дискретизации. Сравните, при построении этой функции для стержневого элемента нам потребовался полином 1-й степени (описывается двумя параметрами), что соответствовало двум деформирующим осевым перемещениям на концах стержня.
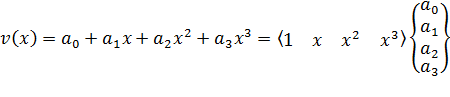. (12)
Применяя (12) в узлах дискретизации, получим:
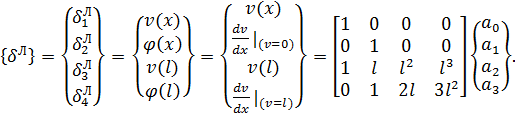(13)
Запишем выражение (13) в матричном виде и используем его для определения столбца параметров 
через столбец узловых перемещений КЭ в локальной системе координат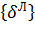 
:
.
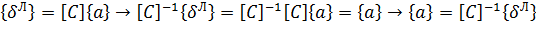Обращение матрицы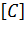 
проводится через матрицу алгебраических дополнений 
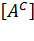матрицы 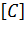по формуле:
;
; 
.
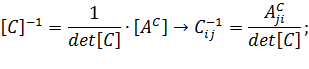
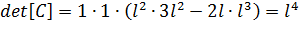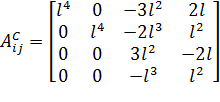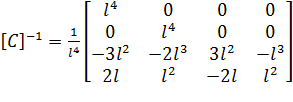Обратите внимание на соотношение индексов элементов обратной матрицы и элементов матрицы алгебраических дополнений – i j и j i соответственно.
Таким образом, согласно (12), имеем:
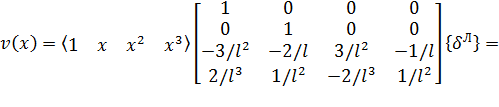
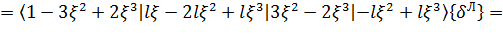
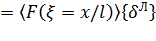. (14)
Здесь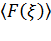 
– матрица интерполяционных функций (функций формы) балочного конечного элемента, преобразованная заменой переменных к зависимости от безразмерной переменной 
.
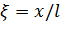4.2. Матрица жесткости балочного конечного элемента
Получение матрицы усилий в узлах конечного элемента проведем на основании формул механики материалов, связывающих функцию поперечного прогиба с изгибающим моментом и изгибающий момент с поперечным усилием, учитывая, что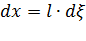 
:
|
|
|
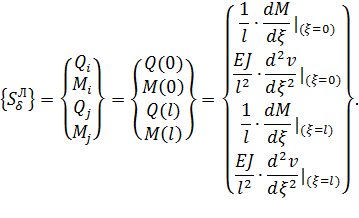
Символ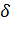 
здесь подчеркивает, что усилия возникают вследствие деформирующих перемещений. Из этих соотношений, используя формулы (14), нетрудно получить соответствующие компоненты матрицы узловых усилий. При этом следует обратить внимание на то, что подобная матрица содержит усилия, которые не отражают условия равновесия балочного КЭ, а потому не может быть окончательным выражением.
Выполняя, тем не менее, предписанные упомянутыми формулами преобразования, получаем:
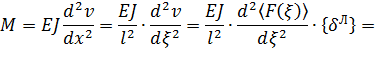
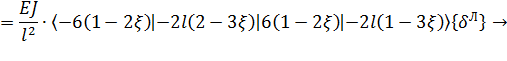
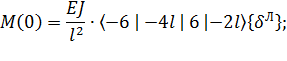
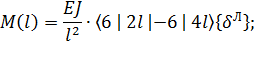
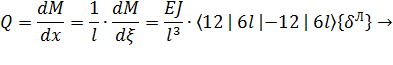
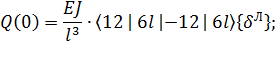
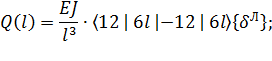
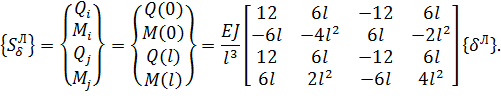
(15)
Полученное выражение позволяет дать интерпретацию матрицы связи векторов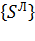 
и 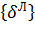: каждый столбец этой матрицы содержит реакции в опорных узлах КЭ при нагружении элемента единичным перемещением в одном из концевых узлов.
На рис. 12 показаны реакции балочного КЭ, нагруженного положительными единичными перемещениями в узле i и находящегося в равновесии. Эпюры при нагружении единичными перемещениями концевых сечений балки нами использовались при изучении метода перемещений.
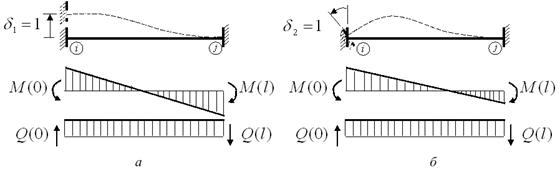
Рис. 12. Реакции балочного КЭ
на единичные узловые перемещения
Сравнение знаков концевых усилий на эпюре рис. 12, а, которая соответствует первому столбцу в матрице (15), и усилий на эпюре рис. 12, б, которая соответствует второму столбцу в матрице, показывает, что знаки усилий во 2-й и 3-й строках полученной матрицы связи следует поменять на противоположные.
Поскольку эпюры рис. 12 получены для балки, находящейся в равновесии.
Таким образом,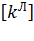 
– матрица жесткости балочного КЭ в локальной системе координат – приобретает вид симметричной матрицы:
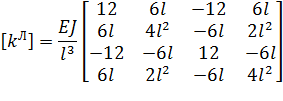
(16)
4.3. Связь величин, заданных в локальной и глобальной системах координат
На рис. 13 представлена исходная информация для получения формул перехода для из ЛСК в ГСК (рис. 13, а) и наоборот (рис. 13, б) для вектора, направленного вдоль оси x в ЛСК.
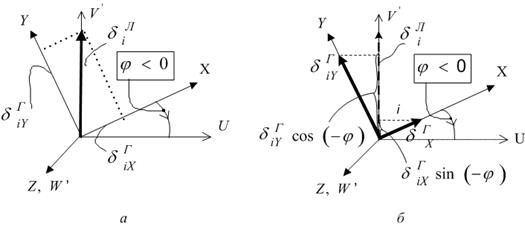
Рис. 13. Связь компонентов вектора в локальной и глобальной системах координат
на Рис.13 заменить название осей U 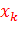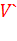на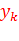 
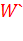на 
на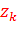 
В соответствии с обозначениями на рис. 13, а можно записать:
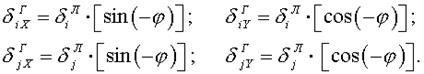
Аналогичные соотношения по рис. 13, б имеют вид:
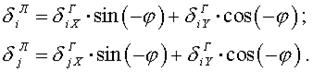
Поскольку повороты в узлах КЭ совершаются вокруг оси Z ГСК, которая совпадает с осью 
ЛСК, и обе оси ортогональны плоскости расчетной схемы, то при переходе из одной системы в другую эти углы не претерпевают никаких изменений.
С учетом сделанного замечания матрицы преобразования из ЛСК в ГСК и обратно могут быть записаны в форме:
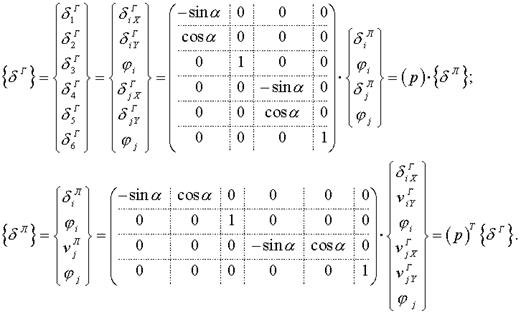(17)
Как следует из вида соотношения (17), они не отличаются от формул аналогичного назначения, которые были получены для стержневого КЭ. Таким образом, имеет место независимость матричных соотношений, определяющих связь компонент матриц в локальной и глобальной системах координат, от размера матриц. По этой же причине справедливы и формулы для вычисления характеристик НДС при переходе из одной системы координат в другую. Наконец, уравнения разрешающей системы уравнений МКЭ в окончательном виде также не содержат ссылок на размеры матриц, которые связаны этими соотношениями. Поэтому для балочного элемента эти уравнения можно использовать так же, как мы это делали для стержневого КЭ.
