Основные теоретические положения

СОДЕРЖАНИЕ

1. Основные теоретические положения                                                                3

2. Содержание задания                                                                                          5

3. Пример выполнения задания                                                                            5

4. Требования к отчету по работе                                                                         6

Контрольные вопросы                                                                                       6

Библиографический список                                                                               6

Приложение А                                                                                                     7

Цель работы: приобрести практические навыки автоматизации статистической обработки данных средствами математического пакета Maple 7.

 

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Как известно, полное описание случайной величины с вероятностной точки зрения дает функция распределения. Однако для решения многих практических задач бывает достаточно указать только отдельные числовые параметры, характеризующие существенные черты распределения: среднее, около которого группируются возможные значения случайной величины; характеристику разброса этих значений относительно среднего и т. д. Такие параметры называют числовыми характеристиками случайной величины. Наиболее часто применяются следующие из них:

1. Математическое ожидание случайной величины.

Для дискретной случайной величины Х, принимающей возможные значения х₁, х₂, …, х_m с вероятностями р₁, р₂, …, р_m, математическое ожидание определяется по формуле:

.

 

Для непрерывной случайной величины математическое ожидание определяется из выражения:

,

 

где f(x) – плотность распределения величины Х.

Если все значения случайной величины неизвестны, по ограниченной выборке значений Х объемом n, можно получить оценку математического ожидания М^*[X] – среднее арифметическое значение случайной величины. При большом числе опытов среднее арифметическое приближается (сходится по вероятности) к математическому ожиданию.

Математическое ожидание иначе называют первым начальным моментом. Вообще говоря, на практике часто применяются моменты двух видов: начальные и центральные. Начальным моментом порядка s случайной величины Х на-

4

зывается математическое ожидание s-й степени этой случайной величины. Для дискретной случайной величины расчетное выражение имеет вид:

 

;

 

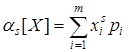для непрерывной –

.

 

Центральным моментом порядка s случайной величины Х называется математическое ожидание s-й степени соответствующей центрированной случайной величины, т.е. величины, из которой вычли ее математическое ожидание:

 

.

 

Для дискретной случайной величины расчетное выражение имеет вид:

 

;

 

для непрерывной –

.

 

Среди центральных моментов важнейшее место занимает второй, называемый дисперсией.

2. Дисперсия случайной величины.

Дисперсия случайной величины Х – математическое ожидание квадрата соответствующей центрированной величины. Она характеризует разброс значений случайной величины около математического ожидания. Вычисляется дисперсия по формулам:

 

,

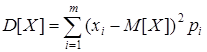– для дискретных и непрерывных случайных величин соответственно.

Дисперсия имеет размерность квадрата случайной величины. Для характеристики рассеяния удобнее пользоваться параметром, размерность которого совпадает с размерностью случайной величины. Таким параметром служит среднее квадратическое отклонение случайной величины:

 

.

 

Для получения оценки дисперсии по ограниченной выборке используют формулу:

5

.

 

3. Характеристика асимметрии распределения случайной величины.

Если распределение симметрично относительно математического ожидания, то все центральные моменты равны нулю. Поэтому для характеристики асимметрии распределения выбран третий центральный момент. Он имеет размерность куба случайной величины. На практике чаще используют безразмерную характеристику – коэффициент асимметрии, или скошенность:

 

.

 

4. Характеристика островершинности распределения.

Остро- или плосковершинность распределения характеризует четвертый центральный момент. На практике используют величину, называемую эксцессом и определяемую по формуле:

 

.

 

Число 3 вычитается из отношения m⁴/s⁴ потому, что для распространенного в природе нормального распределения это отношение равно 3. Т.о. для нормального закона скошенность равна нулю, т.к. это распределение симметрично, и эксцесс также равен нулю.

 

СОДЕРЖАНИЕ ЗАДАНИЯ

 

Для набора данных по указанию преподавателя, средствами математического пакета Maple 7, используя пример, приведенный ниже, и электронный помощник, составить программу и выполнить расчет следующих числовых характеристик случайной величины Х: первый начальный момент, второй, третий, четвертый центральный моменты, среднее квадратическое отклонение, коэффициент асимметрии (скошенность) и эксцесс.