Нормальные алгоритмы Маркова являются еще одной формализацией интуитивного понимания алгоритма. Теория нормальных алгоритмов была создана в конце 40-х — начале 50-х гг. XX в. советским математиком Андреем Андреевичем Марковым (1903 —1979), который называл их нормальными алгоритмами. Класс всех нормально вычислимых функций, т.е. функций, вычислимых с помощью таких алгоритмов, совпадает с классом всех функций, вычислимых по Тьюрингу.
Пусть нам задан алфавит – совокупность (конечная) попарно – различных символов А = {a1, a2, a3, …, an, …}. Символы ai, составляющие алфавит, называются буквами.
Определение 1. Словом в алфавите А называется любая конечная последовательность букв, записанных подряд слева направо.
Примеры: а) Записи любого натурального числа в десятичном счислении 21, 3, 321, 1101 есть примеры слов в алфавите А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
б) Пусть А = {0, 1}. Тогда любое двоичное число 000, 001, 0010, 1101, 1111, … задаёт слово в этом алфавите.
в) Если алфавит А = {а, b, с}, то тогда словами будут следующие наборы: аbcc,cbbabbc, b, bbb,  (знак
(знак 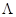 - означает пустое слова, не содержащие ни одной буквы).
- означает пустое слова, не содержащие ни одной буквы).
Определение 2. Количество букв в слове называется длиной слова. Длина пустого слова равна нулю.
Определение 3. Два слова P и Q в одном и том же алфавите А называется равными (обозначается P = Q), если они одинаково записаны т.е. на соответствующих позициях стоят одинаковые буквы.
Определение 4. Композицией двух слов P и Q в одном алфавите А называется новое слово в том же алфавите, которое получается приписываем к слову P справа слова Q и обозначается P 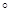 Q (или PQ).
Q (или PQ).
Например, если P = 2131 и Q = 965, то QP = 9652131, PQ=2131965.
Очевидно операция композиции слов не коммутативно (PQ  PQ), но ассоциативна т. е. если даны три слова P, Q и R в одном алфавите А, то (P
PQ), но ассоциативна т. е. если даны три слова P, Q и R в одном алфавите А, то (P  Q)
Q)  R = P
R = P 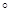 (Q
(Q  R) = PQR.
R) = PQR.
Например, P = 231, Q = 453, R = 19, тогда (P  Q)
Q) 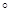 R = (231
R = (231 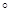 453)
453) 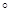 19 = 231453
19 = 231453  19 = 23145319; P
19 = 23145319; P  (Q
(Q 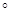 R) = 231
R) = 231 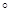 (453
(453  19)= 231
19)= 231  45319 = 23145319.
45319 = 23145319.
Определение 5. Пусть нам даны два слова P и Q в алфавите А. Говорят, что слово Р входит в слово Q (или слово Q содержит слово Р), если слово Q представимо в виде композиции Q = RPS, где R или S – быть может пустые слова.
Например, слово 12 входит в слово 241291247, причем 2 раза.
Очевидно, что каждое слово содержит себя и пустое слово 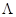 входит в любое другое слово.
входит в любое другое слово.
Если слово Р входит в слово Q несколько раз, то тогда говорят о первом, втором и т. д. вхождениях, обозревая слово Q слева направо.
Определение 6. Марковская подстановка — это операция над словами Р и Q в данном алфавите А, которая задается с помощью упорядоченной пары слов (Р, Q) и состоит в том, что в заданном слове R находят первое вхождение слова Ρ (если таковое имеется) и, не изменяя остальных частей слова R, заменяют в нем это вхождение словом Q.
Полученное слово называется результатом применения марковской подстановки (Р, Q) к слову R. Если же первого вхождения слова Ρ в слове R нет (и, следовательно, нет вообще ни одного вхождения Ρ в Р), то считается, что марковская подстановка (Р, Q) не применима к слову R. Марковскую подстановку, задаваемую с помощью упорядоченной пары слов (Р, Q), обозначают Ρ –> Q.
В связи с возможностью рассмотрения пустых слов возникает вопрос, что значит марковская подстановка 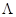 –> ν, т.е. что значит в данное слово w подставить слово υ вместо первого вхождения в w пустого слова
–> ν, т.е. что значит в данное слово w подставить слово υ вместо первого вхождения в w пустого слова 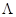 ? По определению полагают, что результатом указанной подстановки является слово vw.
? По определению полагают, что результатом указанной подстановки является слово vw.
Определение 7. Алгоритмом по Маркову (нормальным алгоритмом) называется упорядоченная конечная совокупность марковских подстановок в алфавите А
1) P1→Q1; 2) P2→Q2;…; n) Pn→Qn; (1)
которая определяет следующее правило построения последовательности R слов в алфавите А, исходя из данного слова R в этом алфавите.
Указанная совокупность марковских подстановок (1) называется схемой или записью нормального алгоритма.
Алгоритм предписывает, отправляясь от заданного слова R, просмотреть ориентированные подстановки в порядке возрастания их номеров, разыскивая подстановку с наименьшим номером i (Pi→Qi), левая часть которой Pi входит в слово R. Если такой подстановки не найдется, то процесс прекращается. В противном случае берется самое левое вхождение Pi в R и оно заменяется Qi. При этом слово R преобразуется в слово R1. Далее, вместо слова R берется слово R1,и процесс начинается сначала. Так поступают до тех пор, пока процесс не прекратится. А это может произойти в двух случаях:
1) К полученному слову Rk не применима ни одна из данных подстановок;
2) Когда при получении слова Rk применена подстановка с меткой, т.е. заключительная подстановка (ее будем метить справа точкой).
При этом считается, что данный алгоритм слово R переработал в слово Rk.
Если процесс переработки слова R ни при каком то шаге обрывается, то говорят, что алгоритм к слову R не применим (результат не определен).
Пример. Пусть в алфавите A2={a,b,c} задана система ориентированных подстановок:
1. cb → cc
2. cca → ab
3. ab → bca
4. ca →Λ
Этот алгоритм, будучи применен к слову c abc, никогда не обрывается:
 - получилось первоначальное слово, т.е. алгоритм закончился.
- получилось первоначальное слово, т.е. алгоритм закончился.
Если же брать слово baaacca, то после нескольких шагов процесс оборвется на слове bb:
 .
.
Два нормальных алгоритма отличаются друг от друга алфавитом и системой упорядоченных подстановок или даже только порядком подстановок.
Пример. Пусть в одном и том же алфавите заданы два нормальных алгоритма I1 и I2, отличающиеся друг от друга только порядком подстановок:
I1:
- ab→bac
- ac→ca
- aa→Λ
- bc →bb
- bb→Λ
I2:
1. bc→bb
2. ab→bac
3. ac→ca
4. aa→Λ
5. bb→Λ
Покажем, что I1(abbc)≠I2(abbc):
I1(ab bc)  b ac bc
b ac bc  bc ab c
bc ab c  bcb ac c
bcb ac c  bcbc ac
bcbc ac  bc bcca
bc bcca  bb bc ca
bb bc ca  bbb bc a
bbb bc a 
 bbbb ba
bbbb ba  …
…  ba.
ba.
I2(ab bc)  ab bb
ab bb  b ac bb
b ac bb  bc abb
bc abb  bb ab b
bb ab b  bbb ac b
bbb ac b  bb bc ab
bb bc ab  bbbb ab
bbbb ab 
 bbbbb ac
bbbbb ac  bbbb bc a
bbbb bc a  bbbbbb a
bbbbbb a 

 a.
a. 
Этот пример показывает, что в нормальных алгоритмах имеет значение не только сами подстановки, но и их порядок.
Вычислимые по Маркову функции
Определение 1. Функция y=F(x1,x2,…,xn) называется арифметической функцией, если аргументы xi и значение y принимают только натуральные значения из N={0,1,2,3,…}.
Положительные натуральные числа зададим как слова в однобуквенном алфавите А={1}: пусть число n задается в виде слова из n «единиц».
Построим алгоритм, который любое слово вида  перерабатывает в слово вида
перерабатывает в слово вида 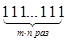 , т.е. вычисляет произведение двух чисел.
, т.е. вычисляет произведение двух чисел.
При этом будем говорить, что функция y=F(x1,x2,…,xn), заданная на некотором множестве слов алфавита А, нормально вычислима, если найдется такой нормальный алгоритм, что каждое слово Ρ (в алфавите А) из области определения функции y=F(x1,x2,…,xn) этот алгоритм перерабатывает в слово y(P) (в алфавите А).
Можно показать, что все известные из арифметики и теории чисел функции вычислимы с помощью нормальных алгоритмов. Это обстоятельство позволило А. Маркову предложить в качестве определения понятия алгоритма нормальный алгоритм.
 2020-04-12
2020-04-12 2872
2872







