| И 1.16 | Определение. Идеальный конденсатор – это элемент электрической цепи, ток в котором пропорционален скорости изменения напряжения; коэффициент пропорциональности называется электрической емкостью конденсатора:
 . (1.3) . (1.3)
|
Комментарий к определению. Если к конденсатору приложено переменное напряжение  , то протекающий через него ток
, то протекающий через него ток  заряжает конденсатор до такой степени, что напряжение созданное его зарядом, уравновешивает приложенное напряжение.
заряжает конденсатор до такой степени, что напряжение созданное его зарядом, уравновешивает приложенное напряжение.
Известно, что заряд конденсатора  пропорционален напряжению между его обкладками,
пропорционален напряжению между его обкладками,
 ,
,
коэффициент пропорциональности  называется емкостью конденсатора. Считая, что к конденсатору приложено переменное напряжение
называется емкостью конденсатора. Считая, что к конденсатору приложено переменное напряжение  и его заряд
и его заряд  изменяется с течением времени, продифференцируем последнее соотношение по времени
изменяется с течением времени, продифференцируем последнее соотношение по времени
 .
.
Изменение заряда конденсатора вызывает электрический ток в проводах, которыми конденсатор присоединен к источнику:
 .
.
Здесь  - заряд конденсатора, а
- заряд конденсатора, а  - заряд, движущийся по проводам к конденсатору, приращения этих величин за любой промежуток времени равны согласно закону сохранения электрического заряда. Следовательно, через конденсатор протекает ток
- заряд, движущийся по проводам к конденсатору, приращения этих величин за любой промежуток времени равны согласно закону сохранения электрического заряда. Следовательно, через конденсатор протекает ток
 .
.
С помощью определения конденсатора в теорию электрических цепей вводится закон сохранения электрического заряда.
Обозначение идеального конденсатора показано на рис. 1.5.

Рис. 1.5. Обозначение идеального конденсатора на схемах цепей
Единица измерения электрической емкости – фарад ( ). Здесь сименс (См) – единица измерения электрической проводимости, величины, обратной сопротивлению.
). Здесь сименс (См) – единица измерения электрической проводимости, величины, обратной сопротивлению.
Зависимость напряжения на конденсаторе от тока получается интегрированием формулы (1.3) по времени от фиксированного момента  до текущего момента
до текущего момента 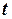 :
:
| И 1.17 |  . (1.4) . (1.4)
|
| И 1.18 | Мгновенная мощность конденсатора
 является алгебраической величиной.
является алгебраической величиной.
|
| И 1.19 | Энергия, запасаемая конденсатором,
 всегда положительна.
всегда положительна.
|
 2020-04-12
2020-04-12 516
516








