Вопрос 3. Следствия из аксиом стереометрии

Простейшие следствия из аксиом будут играть в дальнейшем важную роль. Они почти очевидны, но доказываются.

Следствие 1. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Доказательство. Пусть даны прямая a и не принадлежащая ей точка A.

Выберем на прямой a любые точки B и C.

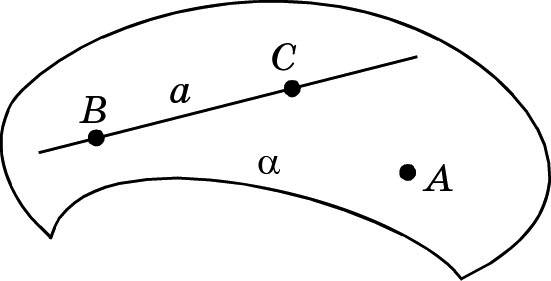
Через точки B и C проходит только одна прямая — прямая a. Так как точка A по условию теоремы не принадлежит прямой a, то точки A, B и C не принадлежат одной прямой.

По аксиоме R ₂ через точки A, B и C проходит только одна плоскость — плоскость ABC, которую обозначим α. Прямая a имеет с ней две общие точки — точки B и C, следовательно, по аксиоме R ₄ эта прямая лежит в плоскости α. Таким образом, плоскость α проходит через прямую a и точку A и является искомой.

Докажем, что другой плоскости, проходящей через прямую a и точку A  ∉  a, не существует.

Предположим, что есть другая плоскость — α₁, проходящая через точку A и прямую a. Тогда плоскости α и α₁ проходят через точки A, B и C, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственная. Теорема доказана.

Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.

Следствие 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

Доказательство. Пусть данные прямые a и b пересекаются в точке C.

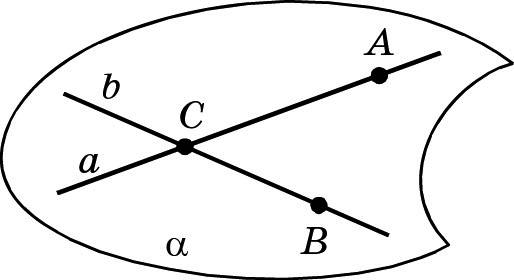
Выберем на прямых a и b любые точки A и B, отличные от C: A  ∈  a, B  ∈  b. Тогда три точки A, B и C не принадлежат одной прямой (почему?), и по аксиоме R ₂ через них можно провести только одну плоскость. Обозначим её α.

Точки A и C прямой a принадлежат плоскости α, значит, плоскость α проходит через прямую a (аксиома R ₄). Плоскость α проходит и через прямую b, так как точки B и C этой прямой принадлежат плоскости α.

Таким образом, плоскость α проходит через прямые a и b, следовательно, является искомой.

Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые a и b, плоскость β.

Так как плоскость β проходит через прямую a и не принадлежащую ей точку B, то по теореме 1 она совпадает с плоскостью α. Единственность плоскости α доказана. ▼

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Если прямые a и b параллельны, то пишут a  ‖  b.

Следствие 3. Через две параллельные прямые можно провести единственную плоскость.

Доказательство. Пусть a и b — данные параллельные прямые. Из определения параллельных прямых следует, что через прямые a и b можно провести плоскость. Обозначим её α и убедимся, что она единственна.

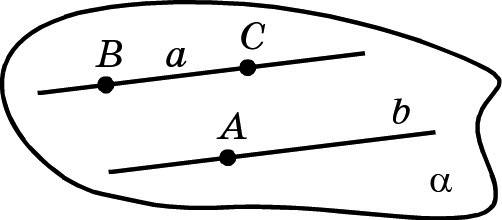
Допустим противное. Пусть существует другая плоскость, отличная от α, которая содержит каждую из прямых a и b. Обозначим эту плоскость β.

Выберем на прямой a точки B и C, на прямой b — точку A. В силу параллельности прямых a и b точки A, B и C не принадлежат одной прямой.

Каждая из плоскостей α и β содержит обе прямые a и b, значит, каждая из них проходит через точки A, B и C. Но по аксиоме R ₂ через эти точки можно провести лишь одну плоскость. Следовательно, плоскости α и β совпадают. Теорема доказана. ▼

Из аксиомы R ₂ и теорем 1, 2 и 3 следует, что плоскость в пространстве можно задать:

Ÿ тремя точками, не принадлежащими одной прямой;

Ÿ прямой и не принадлежащей ей точкой;

Ÿ двумя пересекающимися прямыми;

Ÿ двумя параллельными прямыми.

В дальнейшем вы узнаете, что задать плоскость в пространстве можно и другими определяющими её элементами.

Применяя аксиомы стереометрии и первые следствия из них, вы сможете решать стереометрические задачи, т. е. задачи, в которых исследуются некоторые свойства геометрических фигур, расположенных в пространстве. К стереометрическим относятся, например, задачи на построение сечений многогранников плоскостями.

Сечением многогранника плоскостью является многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости, плоскость при этом называется секущей плоскостью.

Как уже говорилось при обсуждении аксиомы R ₅, плоскость не может пересечь грань многогранника по ломаной, а имеет с ней либо общий отрезок, либо общую точку (вершину многогранника), либо не имеет с ней общих точек. Число сторон многоугольника-сечения не может превышать числа граней многогранника. Причём если пересечением плоскости и многогранника является точка (вершина многогранника) или отрезок (ребро многогранника), то эту плоскость не будем называть секущей.